Difference between revisions of "2024 IMO Problems/Problem 4"
(→Solution simple) |
|||
| (11 intermediate revisions by 7 users not shown) | |||
| Line 8: | Line 8: | ||
==Video Solution== | ==Video Solution== | ||
https://youtu.be/WnZv3fdpFXo | https://youtu.be/WnZv3fdpFXo | ||
| + | |||
| + | ==Video Solution (AI solution)== | ||
| + | https://youtu.be/cjnJ6EXKWW4 | ||
| + | |||
| + | |||
| + | ==Video Solution(In Chinese)== | ||
| + | https://youtu.be/QphkkutmY5M | ||
| + | |||
| + | ==Video Solution== | ||
| + | Part 1: Derive tangent values <math>\angle AIL</math> and <math>\angle AIK</math> with trig values of angles <math>\frac{A}{2}</math>, <math>\frac{B}{2}</math>, <math>\frac{C}{2}</math> | ||
| + | |||
| + | https://youtu.be/p_AmooMMln4 | ||
| + | |||
| + | Part 2: Derive tangent values <math>\angle XPM</math> and <math>\angle YPM</math> with side lengths <math>AB</math>, <math>BC</math>, <math>CA</math>, where <math>M</math> is the midpoint of <math>BC</math> | ||
| + | |||
| + | https://youtu.be/MgrghZ2ESAg | ||
| + | |||
| + | Part 3: Prove that <math>\angle AIL + \angle XPM = 90^\circ</math> and <math>\angle AIK + \angle YPM = 90^\circ</math>. | ||
| + | |||
| + | https://youtu.be/iOp9mnmZyzU | ||
| + | |||
| + | Comments: Although this is an IMO problem, the skills needed to solve this problem have all previously tested in AMC and its system math contests, such as HMMT.~ also proved by Kislay Kai | ||
| + | |||
| + | Evidence 1: 2020 Spring HMMT Geometry Round Problem 8 | ||
| + | |||
| + | I used the property that because point <math>P</math> is on the angle bisector <math>AI</math>, <math>\triangle BPC</math> is isosceles. This is a crucial step to analyze <math>\angle XPY</math>. This technique was previously tested in this HMMT problem. | ||
| + | |||
| + | Evidence 2: 2022 AMC 12A Problem 25 | ||
| + | |||
| + | The technique in this AMC problem can be easily and directly applied to this IMO problem to quickly determine the locations of points <math>X</math> and <math>Y</math>. If you read my solutions to both this AMC problem and this IMO problem, you will find that I simply took exactly the same approach to solve both. | ||
| + | |||
| + | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | |||
| + | ==Video Solution with discussion of a generalized case== | ||
| + | |||
| + | https://youtu.be/NJc79Ccg82E?si=J0YdHAz-46miJIO2 | ||
| + | |||
| + | ==Solution simple== | ||
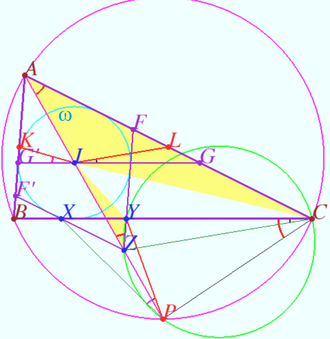
| + | [[File:2024 AIME II 12 d.png|330px|right]] | ||
| + | Let point <math>Z</math> be <math>YZ||AB, XZ||AC, G \in AC, IG||BC, G' \in AB, IG' || BC.</math> | ||
| + | <math>F= AC \cap YZ, F' = AB \cap XZ.</math> | ||
| + | |||
| + | <math>AFZF'</math> is the parallelogram with equal heights, so <math>AFZF'</math> is rhomb <math>\implies</math> | ||
| + | <cmath>\angle CAZ = \angle AZY = \angle BCP, AI = IZ.</cmath> | ||
| + | <cmath>AL = LC, AI = IZ \implies IL || ZC \implies \angle LIG = \angle BCZ.</cmath> | ||
| + | <math>\angle AZY = \angle BCP = \angle YCP \implies</math> points <math>C,P, Y,</math> and <math>Z</math> are concyclic. | ||
| + | |||
| + | Therefore <math>\angle ZPY = \angle LIG.</math> | ||
| + | |||
| + | Similarly, <math>\angle ZPX = \angle KIG'. \blacksquare</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/6J7KH778ptg | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | {{IMO box|year=2024|num-b=3|num-a=5}} | ||
Latest revision as of 20:48, 30 September 2024
Let ![]() be a triangle with
be a triangle with ![]() . Let the incentre and incircle of triangle
. Let the incentre and incircle of triangle
![]() be
be ![]() and
and ![]() , respectively. Let
, respectively. Let ![]() be the point on line
be the point on line ![]() different from
different from ![]() such that the line
through
such that the line
through ![]() parallel to
parallel to ![]() is tangent to
is tangent to ![]() . Similarly, let
. Similarly, let ![]() be the point on line
be the point on line ![]() different from
different from
![]() such that the line through
such that the line through ![]() parallel to
parallel to ![]() is tangent to
is tangent to ![]() . Let
. Let ![]() intersect the circumcircle of
triangle
intersect the circumcircle of
triangle ![]() again at
again at ![]() . Let
. Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() , respectively.
Prove that
, respectively.
Prove that ![]() .
.
Contents
Video Solution
Video Solution (AI solution)
Video Solution(In Chinese)
Video Solution
Part 1: Derive tangent values ![]() and
and ![]() with trig values of angles
with trig values of angles ![]() ,
, ![]() ,
, ![]()
Part 2: Derive tangent values ![]() and
and ![]() with side lengths
with side lengths ![]() ,
, ![]() ,
, ![]() , where
, where ![]() is the midpoint of
is the midpoint of ![]()
Part 3: Prove that ![]() and
and ![]() .
.
Comments: Although this is an IMO problem, the skills needed to solve this problem have all previously tested in AMC and its system math contests, such as HMMT.~ also proved by Kislay Kai
Evidence 1: 2020 Spring HMMT Geometry Round Problem 8
I used the property that because point ![]() is on the angle bisector
is on the angle bisector ![]() ,
, ![]() is isosceles. This is a crucial step to analyze
is isosceles. This is a crucial step to analyze ![]() . This technique was previously tested in this HMMT problem.
. This technique was previously tested in this HMMT problem.
Evidence 2: 2022 AMC 12A Problem 25
The technique in this AMC problem can be easily and directly applied to this IMO problem to quickly determine the locations of points ![]() and
and ![]() . If you read my solutions to both this AMC problem and this IMO problem, you will find that I simply took exactly the same approach to solve both.
. If you read my solutions to both this AMC problem and this IMO problem, you will find that I simply took exactly the same approach to solve both.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution with discussion of a generalized case
https://youtu.be/NJc79Ccg82E?si=J0YdHAz-46miJIO2
Solution simple
Let point ![]() be
be ![]()
![]()
![]() is the parallelogram with equal heights, so
is the parallelogram with equal heights, so ![]() is rhomb
is rhomb ![]()
![]()
![]()
![]() points
points ![]() and
and ![]() are concyclic.
are concyclic.
Therefore ![]()
Similarly, ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
See Also
| 2024 IMO (Problems) • Resources | ||
| Preceded by Problem 3 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 5 |
| All IMO Problems and Solutions | ||