Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 IMO Problems/Problem 4"
(→‎Solution simple)
 
(7 intermediate revisions by 6 users not shown)
Line 7: Line 7:
 
.
 
.
 
==Video Solution==
 
==Video Solution==
−
https://www.youtube.com/watch?v=QphkkutmY5M&t=1s
+
https://youtu.be/WnZv3fdpFXo
 +
 
 +
==Video Solution (AI solution)==
 +
https://youtu.be/cjnJ6EXKWW4
 +
 
  
−
==Video Solution==
+
==Video Solution(In Chinese)==
−
https://youtu.be/WnZv3fdpFXo
+
https://youtu.be/QphkkutmY5M
  
 
==Video Solution==
 
==Video Solution==
Line 25: Line 29:
 
https://youtu.be/iOp9mnmZyzU
 
https://youtu.be/iOp9mnmZyzU
  
−
Comments: Although this is an IMO problem, the skills needed to solve this problem have all previously tested in AMC and its system math contests, such as HMMT.
+
Comments: Although this is an IMO problem, the skills needed to solve this problem have all previously tested in AMC and its system math contests, such as HMMT.~ also proved by Kislay Kai
  
 
Evidence 1: 2020 Spring HMMT Geometry Round Problem 8
 
Evidence 1: 2020 Spring HMMT Geometry Round Problem 8
Line 36: Line 40:
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==Video Solution with discussion of a generalized case==
 +
 +
https://youtu.be/NJc79Ccg82E?si=J0YdHAz-46miJIO2
 +
 +
==Solution simple==
 +
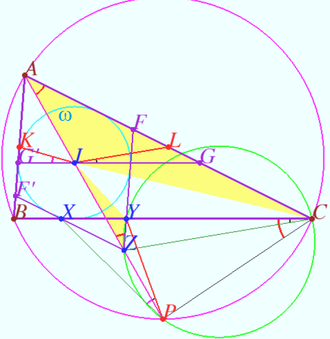
[[File:2024 AIME II 12 d.png|330px|right]]
 +
Let point <math>Z</math> be <math>YZ||AB, XZ||AC, G \in AC, IG||BC, G' \in AB, IG' || BC.</math>
 +
<math>F= AC \cap YZ, F' = AB \cap XZ.</math>
 +
 +
<math>AFZF'</math> is the parallelogram with equal heights, so <math>AFZF'</math> is rhomb <math>\implies</math>
 +
<cmath>\angle CAZ = \angle AZY = \angle BCP, AI = IZ.</cmath>
 +
<cmath>AL = LC, AI = IZ \implies IL || ZC \implies \angle LIG = \angle BCZ.</cmath>
 +
<math>\angle AZY = \angle BCP = \angle YCP \implies</math> points <math>C,P, Y,</math> and <math>Z</math> are concyclic.
 +
 +
Therefore <math>\angle ZPY = \angle LIG.</math>
 +
 +
Similarly, <math>\angle ZPX = \angle KIG'. \blacksquare</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Video Solution==
 +
https://youtu.be/6J7KH778ptg
 +
 +
==See Also==
 +
 +
{{IMO box|year=2024|num-b=3|num-a=5}}

Latest revision as of 20:48, 30 September 2024

Let $ABC$ be a triangle with $AB < AC < BC$. Let the incentre and incircle of triangle $ABC$ be $I$ and $\omega$, respectively. Let $X$ be the point on line $BC$ different from $C$ such that the line through $X$ parallel to $AC$ is tangent to $\omega$. Similarly, let $Y$ be the point on line $BC$ different from $B$ such that the line through $Y$ parallel to $AB$ is tangent to $\omega$. Let $AI$ intersect the circumcircle of triangle $ABC$ again at $P \neq A$. Let $K$ and $L$ be the midpoints of $AC$ and $AB$, respectively. Prove that $\angle KIL + \angle YPX = 180^{\circ}$ .

Video Solution

https://youtu.be/WnZv3fdpFXo

Video Solution (AI solution)

https://youtu.be/cjnJ6EXKWW4


Video Solution(In Chinese)

https://youtu.be/QphkkutmY5M

Video Solution

Part 1: Derive tangent values $\angle AIL$ and $\angle AIK$ with trig values of angles $\frac{A}{2}$, $\frac{B}{2}$, $\frac{C}{2}$

https://youtu.be/p_AmooMMln4

Part 2: Derive tangent values $\angle XPM$ and $\angle YPM$ with side lengths $AB$, $BC$, $CA$, where $M$ is the midpoint of $BC$

https://youtu.be/MgrghZ2ESAg

Part 3: Prove that $\angle AIL + \angle XPM = 90^\circ$ and $\angle AIK + \angle YPM = 90^\circ$.

https://youtu.be/iOp9mnmZyzU

Comments: Although this is an IMO problem, the skills needed to solve this problem have all previously tested in AMC and its system math contests, such as HMMT.~ also proved by Kislay Kai

Evidence 1: 2020 Spring HMMT Geometry Round Problem 8

I used the property that because point $P$ is on the angle bisector $AI$, $\triangle BPC$ is isosceles. This is a crucial step to analyze $\angle XPY$. This technique was previously tested in this HMMT problem.

Evidence 2: 2022 AMC 12A Problem 25

The technique in this AMC problem can be easily and directly applied to this IMO problem to quickly determine the locations of points $X$ and $Y$. If you read my solutions to both this AMC problem and this IMO problem, you will find that I simply took exactly the same approach to solve both.

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution with discussion of a generalized case

https://youtu.be/NJc79Ccg82E?si=J0YdHAz-46miJIO2

Solution simple

2024 AIME II 12 d.png

Let point $Z$ be $YZ||AB, XZ||AC, G \in AC, IG||BC, G' \in AB, IG' || BC.$ $F= AC \cap YZ, F' = AB \cap XZ.$

$AFZF'$ is the parallelogram with equal heights, so $AFZF'$ is rhomb $\implies$ \[\angle CAZ = \angle AZY = \angle BCP, AI = IZ.\] \[AL = LC, AI = IZ \implies IL || ZC \implies \angle LIG = \angle BCZ.\] $\angle AZY = \angle BCP = \angle YCP \implies$ points $C,P, Y,$ and $Z$ are concyclic.

Therefore $\angle ZPY = \angle LIG.$

Similarly, $\angle ZPX = \angle KIG'. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/6J7KH778ptg

See Also

2024 IMO (Problems) • Resources
Preceded by
Problem 3 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 5
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_IMO_Problems/Problem_4&oldid=228698"