Difference between revisions of "Tucker circles"

Latest revision as of 05:34, 4 August 2024

The Tucker circles are a generalization of the cosine circle and first Lemoine circle.

Tucker circle

Let triangle $ABC$ be given. $O$ is it’s circumcenter, $L$ is it’s Lemoine point.

Let homothety centered at $L$ with factor $k$ maps $\triangle ABC$ into $\triangle DEF$ .

Denote the crosspoints of sidelines these triangles as $A' = BC \cap DF, B' = AC \cap DE, C' = AB \cap EF,$ $A'' = BC \cap DE, B'' = AC \cap EF, C'' = AB \cap DF.$

Prove that points $A', B', C', A'', B'',$ and $C''$ lies on the circle centered at $LO$ (Tucker circle).

Proof

$AB' || C''D, AC'' || B'D \implies AB'DC''$ is the parallelogram.

Denote $K = AD \cap B'C'', AK = KD, B'K = KC'' \implies$ $B'C''$ is antiparallel to $BC.$

Similarly, $A''C'$ is antiparallel to $AC, A'B''$ is antiparallel to $AB.$

$M = BE \cap A''C'$ is midpoint $BE, N = A'B'' \cap CF$ is the midpoint $CF.$

$\triangle AB'C'' \sim \triangle ABC.$

$\frac {LD}{AL} = k, AL = LD \implies \frac {AK}{AL} = \frac{2}{k+1}, \frac {KL}{AL} = \frac{1-k}{1+k}.$

Similarly, $\frac {BM}{BL} = \frac {CN}{CL} = \frac {AK}{AL} =\frac{2}{k+1}, \frac {KL}{AL} = \frac{ML}{BM}= \frac {NL}{CL} = \frac{1-k}{1+k}.$

Let $B'''C'''$ be the symmedian $BC$ through $L.$ $B'''C''' || B'C'' \implies B'C'' = B'''C''' \cdot \frac {AK}{AL} =\frac{2B'''C'''}{k+1}.$

It is known that three symmedians through $L$ are equal, so $A''C' = C''B' = B''A' = \frac{2B'''C'''}{k+1}.$

$\triangle KMN$ is homothetic to $\triangle ABC$ with center $L$ and factor $\frac{1-k}{1+k}.$

So segments $A''C' = C''B' = B''A'$ are tangents to $\odot KMN$ and points of contact are the midpoints of these segments.

Denote $Q$ the circumcenter of $\triangle KMN, Q \in LO.$

Therefore $A'Q = B'Q = C'Q = A''Q = B''Q = C''Q. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Tucker circle 2

Let triangle $ABC$ be given. Let $D$ be the arbitrary point on sideline $AC.$

Let $DD'$ be the antiparallel to side $AB, D' \in BC.$

Denote point $E \in AB, D'E || AC.$

Let $EE'$ be the antiparallel to side $BC, E' \in AC.$

Denote point $F \in BC, E'F || AB.$

Let $FF'$ be the antiparallel to side $AC, F' \in AB.$

Prove that points $D, D', E, E', F,$ and $F'$ lies on the circle centered at $LO$ (Tucker circle).

Proof

$\angle ABC = \angle CDD' = \angle AE'E, DE' || DE' \implies DD'EE'$ is isosceles trapezoid.

So $DD' = EE'.$

$\angle ACB = \angle BF'F = \angle AEE', FE' || EF' \implies EFE'F'$ is isosceles trapezoid.

So $FF' = EE' = DD'. \angle BFF' = \angle CD'D \implies F'D || BC.$

Denote $A'$ the midpoint $EE', B'$ the midpoint $FF', C'$ the midpoint $DD'.$ $AB || FE' \implies A'B' ||AB.$ Similarly, $A'C' ||AC, C'B' ||CB.$

$A'$ is the midpoint of antiparallel of $BC \implies AA'$ is the $A-$ symmedian of $\triangle ABC.$

Similarly, $BB'$ is the $B-$ symmedian, $CC'$ is the $C-$ symmedian of $\triangle ABC.$

Therefore Lemoine point $L = AA' \cap BB' \cap CC', \triangle A'B'C'$ is homothetic to $\triangle ABC$ with center $L.$

So segments $DD' = EE' = FF'$ are tangents to $\odot A'B'C'$ and points of contact are the midpoints of these segments.

Denote $Q$ the circumcenter of $\triangle A'B'C', Q \in LO,$ where $O$ is the circumcenter of $\triangle ABC.$

Therefore $DQ = D'Q = EQ = E'Q = FQ = F'Q. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 1: / Line 1: @@
 The Tucker circles are a generalization of the cosine circle and first Lemoine circle.
+==Tucker circle==
+[[File:Tucker circle.png|450px|right]]
+[[File:Tucker circle A.png|450px|right]]
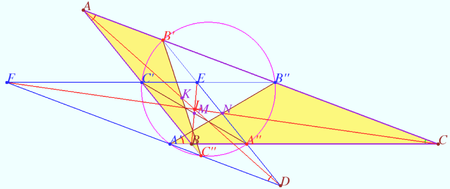
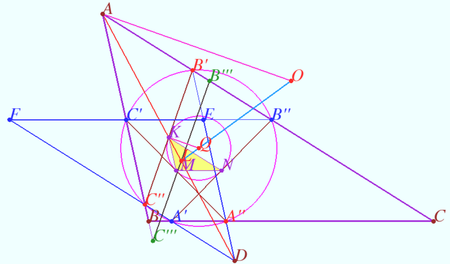
+Let triangle <math>ABC</math> be given. <math>O</math> is it’s circumcenter, <math>L</math> is it’s Lemoine point.
+Let homothety centered at <math>L</math> with factor <math>k</math> maps <math>\triangle ABC</math> into <math>\triangle DEF</math>.
+Denote the crosspoints of sidelines these triangles as
+<cmath>A' = BC \cap DF, B' = AC \cap DE, C' = AB \cap EF,</cmath>
+<cmath> A'' = BC \cap DE, B'' = AC \cap EF, C'' = AB \cap DF.</cmath>
+Prove that points <math>A', B', C', A'', B'',</math> and <math>C''</math> lies on the circle centered at <math>LO</math> (Tucker circle).
+<i><b>Proof</b></i>
+<math>AB' || C''D, AC'' || B'D \implies AB'DC''</math> is the parallelogram.
+Denote <math>K = AD \cap B'C'', AK = KD, B'K = KC'' \implies</math>
+<math>B'C''</math> is antiparallel to <math>BC.</math>
+Similarly, <math>A''C'</math> is antiparallel to <math>AC, A'B''</math> is antiparallel to <math>AB.</math>
+<math>M = BE \cap A''C'</math> is midpoint <math>BE, N =  A'B'' \cap CF</math> is the midpoint <math>CF.</math>
+<math>\triangle AB'C'' \sim \triangle ABC.</math>
+<math>\frac {LD}{AL} = k, AL = LD \implies  \frac {AK}{AL} = \frac{2}{k+1}, \frac {KL}{AL} = \frac{1-k}{1+k}.</math>
+Similarly, <math>\frac {BM}{BL} = \frac {CN}{CL} = \frac {AK}{AL} =\frac{2}{k+1}, \frac {KL}{AL} = \frac{ML}{BM}=  \frac {NL}{CL} = \frac{1-k}{1+k}.</math>
+Let <math>B'''C'''</math> be the symmedian <math>BC</math> through <math>L.</math>
+<cmath>B'''C''' || B'C'' \implies B'C'' = B'''C''' \cdot  \frac {AK}{AL} =\frac{2B'''C'''}{k+1}.</cmath>
+It is known that three symmedians through <math>L</math> are equal, so <math>A''C' = C''B' = B''A' = \frac{2B'''C'''}{k+1}.</math>
+<math>\triangle KMN</math> is homothetic to <math>\triangle ABC</math> with center <math>L</math> and factor <math>\frac{1-k}{1+k}.</math>
+So segments <math>A''C' = C''B' = B''A'</math> are tangents to <math>\odot KMN</math> and points of contact are the midpoints of these segments.
+Denote <math>Q</math> the circumcenter of <math>\triangle KMN, Q \in LO.</math>
+Therefore <math>A'Q = B'Q = C'Q = A''Q = B''Q = C''Q. \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Tucker circle 2==
+[[File:Tucker circle B.png|440px|right]]
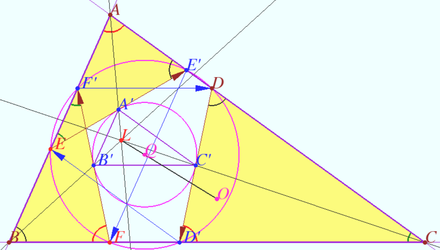
+Let triangle <math>ABC</math> be given. Let <math>D</math> be the arbitrary point on sideline <math>AC.</math>
+Let <math>DD'</math> be the antiparallel to side <math>AB, D' \in BC.</math>
+Denote point <math>E \in AB, D'E || AC.</math>
+Let <math>EE'</math> be the antiparallel to side <math>BC, E' \in AC.</math>
+Denote point <math>F \in BC, E'F || AB.</math>
+Let <math>FF'</math> be the antiparallel to side <math>AC, F' \in AB.</math>
+Prove that points <math>D, D', E, E', F,</math> and <math>F'</math> lies on the circle centered at <math>LO</math> (Tucker circle).
+<i><b>Proof</b></i>
+<math>\angle ABC = \angle CDD' = \angle AE'E, DE' || DE' \implies DD'EE'</math> is isosceles trapezoid.
+So <math>DD' = EE'.</math>
+<math>\angle ACB = \angle BF'F = \angle AEE', FE' || EF' \implies EFE'F'</math> is isosceles trapezoid.
+So <math>FF' = EE' = DD'. \angle BFF' = \angle CD'D \implies F'D || BC.</math>
+Denote <math>A'</math> the midpoint <math>EE', B'</math> the midpoint <math>FF', C'</math> the midpoint <math>DD'.</math>
+<math>AB || FE' \implies A'B' ||AB.</math> Similarly, <math>A'C' ||AC, C'B' ||CB.</math>
+<math>A'</math> is the midpoint of antiparallel of <math>BC \implies AA'</math> is the <math>A-</math>symmedian of <math>\triangle ABC.</math>
+Similarly, <math>BB'</math> is the <math>B-</math>symmedian, <math>CC'</math> is the <math>C-</math>symmedian of <math>\triangle ABC.</math>
+Therefore Lemoine point <math>L = AA' \cap BB' \cap CC', \triangle A'B'C'</math> is homothetic to <math>\triangle ABC</math> with center <math>L.</math>
+So segments <math>DD' = EE' = FF'</math> are tangents to <math>\odot  A'B'C'</math> and points of contact are the midpoints of these segments.
+Denote <math>Q</math> the circumcenter of <math>\triangle  A'B'C', Q \in LO,</math> where <math>O</math> is the circumcenter of <math>\triangle ABC.</math>
+Therefore <math>DQ = D'Q = EQ = E'Q = FQ = F'Q. \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''

Page

Toolbox

Search

Difference between revisions of "Tucker circles"

Latest revision as of 05:34, 4 August 2024

Tucker circle

Tucker circle 2