Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 IMO Problems/Problem 3"

(I just added in the solution to the problem)
m (→‎Solution)
 
(5 intermediate revisions by 2 users not shown)
Line 12: Line 12:
 
==Solution==
 
==Solution==
 
Answer: No. There is no such strategy for the hunter. The rabbit will always “Win”
 
Answer: No. There is no such strategy for the hunter. The rabbit will always “Win”
 +
 
Proof:
 
Proof:
−
Suppose the answer is Yes. Therefore, there exists a strategy for the hunter to always “win” no matter how the rabbit moved or how the radar pinged. We will show that with bad luck from radar pings, the hunter cannot guarantee that the distance stays below <math>100</math> after <math>10^9</math> moves.
+
Suppose on the contrary that the answer is Yes. Therefore, there exists a strategy for the hunter to always “win” no matter how the rabbit moved or how the radar pinged. We will show that with bad luck from radar pings, the hunter cannot guarantee that the distance stays below <math>100</math> after <math>10^9</math> moves.
  
 
Let <math>d_n</math> be the distance be the distance between the hunter and the rabbit after <math>n</math> rounds.  
 
Let <math>d_n</math> be the distance be the distance between the hunter and the rabbit after <math>n</math> rounds.  
 
If <math>d_n \geq 100, n < 10^9,</math> the rabbit has won as all it needs to do is to move straight away from the hunter and the distance between the two will be kept at or above <math>100</math> thereon.
 
If <math>d_n \geq 100, n < 10^9,</math> the rabbit has won as all it needs to do is to move straight away from the hunter and the distance between the two will be kept at or above <math>100</math> thereon.
−
Now we tackle the other case, <math>d_n < 100</math>. We will show that whatever strategy the hunter follows, after <math>200</math> rounds, the rabbit can increase <math>d_n^2</math> by at least <math>\frac{1}{2}</math> with lucky radar pings. This way, <math>d_n^2</math> will reach <math>10^4</math> in less than <math>2\cdot 200 \cdot 10^4 = 4 \cdot 10^6 < 10^9</math> rounds, in which the rabbit wins.
+
Now we tackle the other case, <math>d_n \le 100</math>. We will show that whatever strategy the hunter follows, after <math>200</math> rounds, the rabbit can increase <math>d_n^2</math> by at least <math>\frac{1}{2}</math> with lucky radar pings. This way, <math>d_n^2</math> will reach <math>10^4</math> in less than <math>2\cdot 200 \cdot 10^4 = 4 \cdot 10^6 < 10^9</math> rounds, in which the rabbit wins.
−
Suppose the hunter is at <math>H_n</math> and the rabbit is at <math>R_n</math>. Suppose the rabbit <math>reveals</math> its location (this allow us to ignore all information from previous radar pings).  
+
Suppose the hunter is at <math>H_n</math> and the rabbit is at <math>R_n</math>. Suppose the rabbit <math>\textit{reveals}</math> its location (this allow us to ignore all information from previous radar pings).  
 
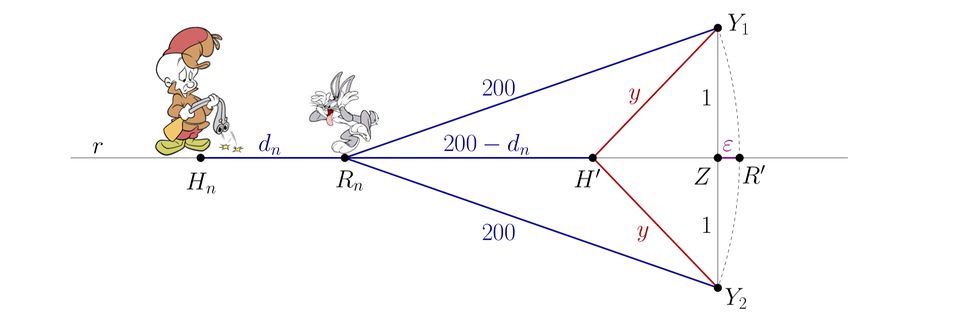
Let <math>r</math> be the line <math>H_n R_n, </math> and let <math>Y_1</math> and <math>Y_2</math> be points which are <math>1</math> unit away from <math>r</math> and <math>200</math> units away from <math>R_n</math>, as in the figure below.
 
Let <math>r</math> be the line <math>H_n R_n, </math> and let <math>Y_1</math> and <math>Y_2</math> be points which are <math>1</math> unit away from <math>r</math> and <math>200</math> units away from <math>R_n</math>, as in the figure below.
−
[img]https://i.imgur.com/Wj996Es.jpeg[/img]
+
 
 +
[[Image: IMO 2017 SL C5 solution graph.jpeg |thumb|left|957px|Picture from the official IMO solution of this problem]]
  
 
The rabbit’s plan is to simply choose one of the points <math>Y_1</math> or <math>Y_2</math> and hop <math>200</math> rounds straight towards it. Since all hops stay within <math>1</math> distance unit from <math>r</math>, it is possible that all radar pings stay on <math>r</math>. In particular, in this case, the hunter has no way of determining whether the rabbit is heading for <math>Y_1</math> or <math>Y_2</math>.
 
The rabbit’s plan is to simply choose one of the points <math>Y_1</math> or <math>Y_2</math> and hop <math>200</math> rounds straight towards it. Since all hops stay within <math>1</math> distance unit from <math>r</math>, it is possible that all radar pings stay on <math>r</math>. In particular, in this case, the hunter has no way of determining whether the rabbit is heading for <math>Y_1</math> or <math>Y_2</math>.
  
−
Looking at these pings, what can the hunter do? His best strategy is to go 200 rounds straight to the right, ending up at point <math>H’</math> in the figure because the hunter will always be to the left of <math>H’</math> after the <math>200</math> rounds, and if the hunter is above <math>r</math>, then he will be further away from <math>Y_2</math>, and if he is below <math>r</math>, then he will be further away from <math>Y_1</math>. In short, he can never be sure that the distance from him and the rabbit will be less than <math>y = H’Y_1 = H’Y_2</math> after these <math>200</math> rounds.
+
Looking at these pings, what can the hunter do? His best strategy is to go <math>200</math> rounds straight to the right, ending up at point <math>H’</math> in the figure because the hunter will always be to the left of <math>H’</math> after the <math>200</math> rounds, and if the hunter is above <math>r</math>, then he will be further away from <math>Y_2</math>, and if he is below <math>r</math>, then he will be further away from <math>Y_1</math>. In short, he can never be sure that the distance from him and the rabbit will be less than <math>y = H’Y_1 = H’Y_2</math> after these <math>200</math> rounds.
−
To estimate <math>y^2</math>, we take <math>Z</math> as the midpoint of segment <math>Y_1Y_2</math>, we take <math>R’</math> as a point <math>200</math> units to the right of <math>R_n</math>, and define <math>\epsilon = ZR’</math> (Note that <math>H’R’ = d_n). Then
+
To estimate <math>y^2</math>, we take <math>Z</math> as the midpoint of segment <math>Y_1Y_2</math>, we take <math>R’</math> as a point <math>200</math> units to the right of <math>R_n</math>, and define <math>\epsilon = ZR’</math> (Note that <math>H’R’ = d_n</math>). Then
−
<cmath> y^2 = 1 + (H’Z)^2 = 1+(d_n-\epsilon)^2
+
<cmath> y^2 = 1 + (H’Z)^2 = 1+(d_n-\epsilon)^2</cmath>
 
Where
 
Where
−
</cmath>\epsilon = 200 - R_nZ = 200 - \sqrt{200^2-1} = \frac{1}{200+\sqrt{200^2-1}} > frac{1}{400}</math><math>.
+
<cmath>\epsilon = 200 - R_nZ = 200 - \sqrt{200^2-1} = \frac{1}{200+\sqrt{200^2-1}} > \frac{1}{400}</cmath>.
−
In particular, </math>\epsilon^2 + 1 = 400\epsilon<math>, so
+
In particular, <math>\epsilon^2 + 1 = 400\epsilon</math>, so
 
<cmath>y^2 = d_n^2 - 2\epsilon d_n + \epsilon^2+1 = d_n^2 + \epsilon(400-2d_n)</cmath>
 
<cmath>y^2 = d_n^2 - 2\epsilon d_n + \epsilon^2+1 = d_n^2 + \epsilon(400-2d_n)</cmath>
−
Since </math>\epsilon > \frac{1}{400}<math> and we assumed </math>d_n < 100<math>, this shows that </math>y^2 > d_n^2 + \frac{1}{2}$. So ,as we claimed, with this list of radar pings, no matter what the hunter does, the rabbit might achieve  
+
Since <math>\epsilon > \frac{1}{400}</math> and we assumed <math>d_n < 100</math>, this shows that <math>y^2 > d_n^2 + \frac{1}{2}</math>. So ,as we claimed, with this list of radar pings, no matter what the hunter does, the rabbit might achieve  
 
<cmath> d_{n+200}^2 > d_n^2 + \frac{1}{2}</cmath>
 
<cmath> d_{n+200}^2 > d_n^2 + \frac{1}{2}</cmath>
 
The rabbit wins.
 
The rabbit wins.
 
~Archieguan
 
~Archieguan
 +
 
==See Also==
 
==See Also==
  
 
{{IMO box|year=2017|num-b=2|num-a=4}}
 
{{IMO box|year=2017|num-b=2|num-a=4}}

Latest revision as of 10:16, 29 October 2024

Problem

A hunter and an invisible rabbit play a game in the Euclidean plane. The rabbit's starting point, $A_0$, and the hunter's starting point, $B_0$, are the same. After $n-1$ rounds of the game, the rabbit is at point $A_{n-1}$ and the hunter is at point $B_{n-1}$. In the nth round of the game, three things occur in order.

(i) The rabbit moves invisibly to a point $A_n$ such that the distance between $A_{n-1}$ and $A_n$ is exactly 1.

(ii) A tracking device reports a point $P_n$ to the hunter. The only guarantee provided by the tracking device is that the distance between $P_n$ and $A_n$ is at most 1.

(iii) The hunter moves visibly to a point $B_n$ such that the distance between $B_{n-1}$ and $B_n$ is exactly 1.

Is it always possible, no matter how the rabbit moves, and no matter what points are reported by the tracking device, for the hunter to choose her moves so that after $10^9$ rounds she can ensure that the distance between her and the rabbit is at most 100?

Solution

Answer: No. There is no such strategy for the hunter. The rabbit will always “Win”

Proof: Suppose on the contrary that the answer is Yes. Therefore, there exists a strategy for the hunter to always “win” no matter how the rabbit moved or how the radar pinged. We will show that with bad luck from radar pings, the hunter cannot guarantee that the distance stays below $100$ after $10^9$ moves.

Let $d_n$ be the distance be the distance between the hunter and the rabbit after $n$ rounds. If $d_n \geq 100, n < 10^9,$ the rabbit has won as all it needs to do is to move straight away from the hunter and the distance between the two will be kept at or above $100$ thereon. Now we tackle the other case, $d_n \le 100$. We will show that whatever strategy the hunter follows, after $200$ rounds, the rabbit can increase $d_n^2$ by at least $\frac{1}{2}$ with lucky radar pings. This way, $d_n^2$ will reach $10^4$ in less than $2\cdot 200 \cdot 10^4 = 4 \cdot 10^6 < 10^9$ rounds, in which the rabbit wins. Suppose the hunter is at $H_n$ and the rabbit is at $R_n$. Suppose the rabbit $\textit{reveals}$ its location (this allow us to ignore all information from previous radar pings). Let $r$ be the line $H_n R_n,$ and let $Y_1$ and $Y_2$ be points which are $1$ unit away from $r$ and $200$ units away from $R_n$, as in the figure below.

Picture from the official IMO solution of this problem

The rabbit’s plan is to simply choose one of the points $Y_1$ or $Y_2$ and hop $200$ rounds straight towards it. Since all hops stay within $1$ distance unit from $r$, it is possible that all radar pings stay on $r$. In particular, in this case, the hunter has no way of determining whether the rabbit is heading for $Y_1$ or $Y_2$.

Looking at these pings, what can the hunter do? His best strategy is to go $200$ rounds straight to the right, ending up at point $H’$ in the figure because the hunter will always be to the left of $H’$ after the $200$ rounds, and if the hunter is above $r$, then he will be further away from $Y_2$, and if he is below $r$, then he will be further away from $Y_1$. In short, he can never be sure that the distance from him and the rabbit will be less than $y = H’Y_1 = H’Y_2$ after these $200$ rounds. To estimate $y^2$, we take $Z$ as the midpoint of segment $Y_1Y_2$, we take $R’$ as a point $200$ units to the right of $R_n$, and define $\epsilon = ZR’$ (Note that $H’R’ = d_n$). Then \[y^2 = 1 + (H’Z)^2 = 1+(d_n-\epsilon)^2\] Where \[\epsilon = 200 - R_nZ = 200 - \sqrt{200^2-1} = \frac{1}{200+\sqrt{200^2-1}} > \frac{1}{400}\]. In particular, $\epsilon^2 + 1 = 400\epsilon$, so \[y^2 = d_n^2 - 2\epsilon d_n + \epsilon^2+1 = d_n^2 + \epsilon(400-2d_n)\] Since $\epsilon > \frac{1}{400}$ and we assumed $d_n < 100$, this shows that $y^2 > d_n^2 + \frac{1}{2}$. So ,as we claimed, with this list of radar pings, no matter what the hunter does, the rabbit might achieve \[d_{n+200}^2 > d_n^2 + \frac{1}{2}\] The rabbit wins. ~Archieguan

See Also

2017 IMO (Problems) • Resources
Preceded by
Problem 2 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 4
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_IMO_Problems/Problem_3&oldid=230807"