Difference between revisions of "2005 USAMO Problems/Problem 1"
I like pie (talk | contribs) (Official solution (image needed)) |
|||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | Determine all composite positive integers <math>n</math> for which it is possible to arrange all divisors of <math>n</math> that are greater than 1 in a circle so that no two adjacent divisors are relatively prime. | + | (''Zuming Feng'') Determine all composite positive integers <math>n</math> for which it is possible to arrange all divisors of <math>n</math> that are greater than 1 in a circle so that no two adjacent divisors are relatively prime. |
== Solution == | == Solution == | ||
| Line 6: | Line 6: | ||
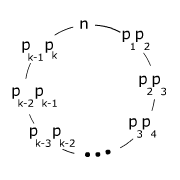
No such circular arrangement exists for <math>n=pq</math>, where <math>p</math> and <math>q</math> are distinct primes. In that case, the numbers to be arranged are <math>p</math>; <math>q</math> and <math>pq</math>, and in any circular arrangement, <math>p</math> and <math>q</math> will be adjacent. We claim that the desired circular arrangement exists in all other cases. If <math>n=p^e</math> where <math>e\ge2</math>, an arbitrary circular arrangement works. Henceforth we assume that <math>n</math> has prime factorization <math>p^{e_1}_{1}p^{e_2}_{2}\cdots p^{e_k}_k</math>, where <math>p_1<p_2<\cdots<p_k</math> and either <math>k>2</math> or else <math>\max(e1,e2)>1</math>. To construct the desired circular arrangement of <math>D_n:=\lbrace d:d|n\ \text{and}\ d>1\rbrace</math>, start with the circular arrangement of <math>n,p_{1}p_{2},p_{2}p_{3}\ldots,p_{k-1}p_{k}</math> as shown. | No such circular arrangement exists for <math>n=pq</math>, where <math>p</math> and <math>q</math> are distinct primes. In that case, the numbers to be arranged are <math>p</math>; <math>q</math> and <math>pq</math>, and in any circular arrangement, <math>p</math> and <math>q</math> will be adjacent. We claim that the desired circular arrangement exists in all other cases. If <math>n=p^e</math> where <math>e\ge2</math>, an arbitrary circular arrangement works. Henceforth we assume that <math>n</math> has prime factorization <math>p^{e_1}_{1}p^{e_2}_{2}\cdots p^{e_k}_k</math>, where <math>p_1<p_2<\cdots<p_k</math> and either <math>k>2</math> or else <math>\max(e1,e2)>1</math>. To construct the desired circular arrangement of <math>D_n:=\lbrace d:d|n\ \text{and}\ d>1\rbrace</math>, start with the circular arrangement of <math>n,p_{1}p_{2},p_{2}p_{3}\ldots,p_{k-1}p_{k}</math> as shown. | ||
| − | + | [[Image:2005_USAMO_1.png]] | |
Then between <math>n</math> and <math>p_{1}p_{2}</math>, place (in arbitrary order) all other members of <math>D_n</math> that have <math>p_1</math> as their smallest prime factor. Between <math>p_{1}p_{2}</math> and <math>p_{2}p_{3}</math>, place all members of <math>D_n</math> other than <math>p_{2}p_{3}</math> that have <math>p_2</math> as their smallest prime factor. Continue in this way, ending by placing <math>p_k,p^{2}_{k},\ldots,p^{e_k}_{k}</math> between <math>p_{k-1}p_k</math> and <math>n</math>. It is easy to see that each element of <math>D_n</math> is placed exactly one time, and any two adjacent elements have a common prime factor. Hence this arrangement has the desired property. | Then between <math>n</math> and <math>p_{1}p_{2}</math>, place (in arbitrary order) all other members of <math>D_n</math> that have <math>p_1</math> as their smallest prime factor. Between <math>p_{1}p_{2}</math> and <math>p_{2}p_{3}</math>, place all members of <math>D_n</math> other than <math>p_{2}p_{3}</math> that have <math>p_2</math> as their smallest prime factor. Continue in this way, ending by placing <math>p_k,p^{2}_{k},\ldots,p^{e_k}_{k}</math> between <math>p_{k-1}p_k</math> and <math>n</math>. It is easy to see that each element of <math>D_n</math> is placed exactly one time, and any two adjacent elements have a common prime factor. Hence this arrangement has the desired property. | ||
''Note.'' In graph theory terms, this construction yields a Hamiltonian cycle in the graph with vertex set <math>D_n</math> in which two vertices form an edge if the two corresponding numbers have a common prime factor. The graphs below illustrate the construction for the special cases <math>n=p^{2}q</math> and <math>n=pqr</math>. | ''Note.'' In graph theory terms, this construction yields a Hamiltonian cycle in the graph with vertex set <math>D_n</math> in which two vertices form an edge if the two corresponding numbers have a common prime factor. The graphs below illustrate the construction for the special cases <math>n=p^{2}q</math> and <math>n=pqr</math>. | ||
| + | |||
| + | |||
| + | === Solution 2 === | ||
| + | The proof that no arrangement exists for <math>n=pq</math>, where <math>p,q</math> are distinct primes follows from above. Apply induction to prove all other cases are possible | ||
| + | |||
| + | Base case: | ||
| + | #<math>n=p^r</math>, where <math>p</math> is a prime and <math>r</math> is a positive integer. Any arrangement suffices | ||
| + | #<math>n=pqr</math>, where <math>p,q,r</math> are distinct primes. The following configuration works | ||
| + | <cmath>p,pq,pr,r,qr,q,pqr</cmath> | ||
| + | Inductive step: Suppose the desired arrangement exists for a composite <math>n</math>, show the arrangement exists for <math>np^r</math>, where <math>p</math> is a prime relatively prime to <math>n</math> and <math>r</math> is a positive integer | ||
| + | |||
| + | Let <math>a_1,a_2,\cdots,a_m</math> be the arrangement of divisors of <math>n</math>, then <math>(a_i,a_{i+1})>1</math> for <math>i=1,2,\cdots,m</math>, where <math>a_{m+1}=a_1</math>. The divisors of <math>np^r</math> greater than 1 are of the form | ||
| + | <cmath>a_ip^j,p^j\qquad 1\leq i\leq m,1\leq j\leq r</cmath> | ||
| + | The following sequence works | ||
| + | <cmath>a_1,\cdots,a_{m-1}, a_{m-1}p,\text{other divisors in arbitrary order},a_mp,a_m</cmath> | ||
| + | since all other divisors are divisible by <math>p</math>. | ||
| + | |||
| + | {{alternate solutions}} | ||
== See also == | == See also == | ||
| + | * <url>viewtopic.php?t=34314 Discussion on AoPS/MathLinks</url> | ||
| + | |||
{{USAMO newbox|year=2005|before=First Question|num-a=2}} | {{USAMO newbox|year=2005|before=First Question|num-a=2}} | ||
[[Category:Olympiad Number Theory Problems]] | [[Category:Olympiad Number Theory Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 12:40, 4 July 2013
Problem
(Zuming Feng) Determine all composite positive integers ![]() for which it is possible to arrange all divisors of
for which it is possible to arrange all divisors of ![]() that are greater than 1 in a circle so that no two adjacent divisors are relatively prime.
that are greater than 1 in a circle so that no two adjacent divisors are relatively prime.
Solution
Solution 1 (official solution)
No such circular arrangement exists for ![]() , where
, where ![]() and
and ![]() are distinct primes. In that case, the numbers to be arranged are
are distinct primes. In that case, the numbers to be arranged are ![]() ;
; ![]() and
and ![]() , and in any circular arrangement,
, and in any circular arrangement, ![]() and
and ![]() will be adjacent. We claim that the desired circular arrangement exists in all other cases. If
will be adjacent. We claim that the desired circular arrangement exists in all other cases. If ![]() where
where ![]() , an arbitrary circular arrangement works. Henceforth we assume that
, an arbitrary circular arrangement works. Henceforth we assume that ![]() has prime factorization
has prime factorization ![]() , where
, where ![]() and either
and either ![]() or else
or else ![]() . To construct the desired circular arrangement of
. To construct the desired circular arrangement of ![]() , start with the circular arrangement of
, start with the circular arrangement of ![]() as shown.
as shown.
Then between ![]() and
and ![]() , place (in arbitrary order) all other members of
, place (in arbitrary order) all other members of ![]() that have
that have ![]() as their smallest prime factor. Between
as their smallest prime factor. Between ![]() and
and ![]() , place all members of
, place all members of ![]() other than
other than ![]() that have
that have ![]() as their smallest prime factor. Continue in this way, ending by placing
as their smallest prime factor. Continue in this way, ending by placing ![]() between
between ![]() and
and ![]() . It is easy to see that each element of
. It is easy to see that each element of ![]() is placed exactly one time, and any two adjacent elements have a common prime factor. Hence this arrangement has the desired property.
is placed exactly one time, and any two adjacent elements have a common prime factor. Hence this arrangement has the desired property.
Note. In graph theory terms, this construction yields a Hamiltonian cycle in the graph with vertex set ![]() in which two vertices form an edge if the two corresponding numbers have a common prime factor. The graphs below illustrate the construction for the special cases
in which two vertices form an edge if the two corresponding numbers have a common prime factor. The graphs below illustrate the construction for the special cases ![]() and
and ![]() .
.
Solution 2
The proof that no arrangement exists for ![]() , where
, where ![]() are distinct primes follows from above. Apply induction to prove all other cases are possible
are distinct primes follows from above. Apply induction to prove all other cases are possible
Base case:
 , where
, where  is a prime and
is a prime and  is a positive integer. Any arrangement suffices
is a positive integer. Any arrangement suffices , where
, where  are distinct primes. The following configuration works
are distinct primes. The following configuration works
![]() Inductive step: Suppose the desired arrangement exists for a composite
Inductive step: Suppose the desired arrangement exists for a composite ![]() , show the arrangement exists for
, show the arrangement exists for ![]() , where
, where ![]() is a prime relatively prime to
is a prime relatively prime to ![]() and
and ![]() is a positive integer
is a positive integer
Let ![]() be the arrangement of divisors of
be the arrangement of divisors of ![]() , then
, then ![]() for
for ![]() , where
, where ![]() . The divisors of
. The divisors of ![]() greater than 1 are of the form
greater than 1 are of the form
![]() The following sequence works
The following sequence works
![]() since all other divisors are divisible by
since all other divisors are divisible by ![]() .
.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See also
- <url>viewtopic.php?t=34314 Discussion on AoPS/MathLinks</url>
| 2005 USAMO (Problems • Resources) | ||
| Preceded by First Question |
Followed by Problem 2 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.