Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 3 Pre 2005 Problems/Problem 14"

m (rough solution)
 
(28 intermediate revisions by 2 users not shown)
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
−
Invert about a circle with radius 1 and center P. Note that since all relevant circles and lines go through P, they all are transformed into lines, and <math>\omega_1,\omega_2, l</math> are all tangent at infinity (i.e. parallel). That was the crux move; some more basic length chasing using similar triangles gets you the answer.
 
−
{{solution}}
 
  
−
==See also==
+
[[File:AIME_2005_14a.png|600px]]
 +
 
 +
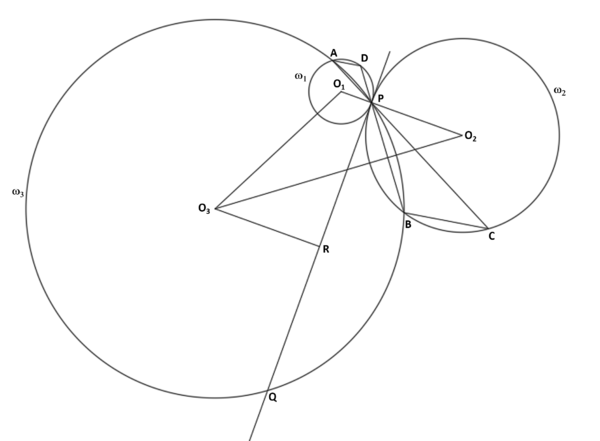
Let <math>O_1, O_2,</math> and <math>O_3</math> be the centers of <math>\omega_1, \omega_2</math> and <math>\omega_3</math> respectively.
 +
 
 +
Let point <math>R</math> be the midpoint of <math>QP</math>.  Thus, <math>O_3R \bot PQ</math> and <math>|PR|=\frac{|PQ|}{2}=16</math>
 +
 
 +
Let <math>r_1</math> and <math>r_2</math> be the radii of circles <math>\omega_1</math> and <math>\omega_2</math> respectively.
 +
 
 +
Let <math>A_1</math> and <math>A_2</math> be the areas of triangles <math>PDA</math> and <math>PBC</math> respectively.
 +
 
 +
Since <math>O_3R \parallel O_1O_2</math> and <math>\angle RO_3O_2 = \angle O_3O_2O_1</math>, then <math>O_2B \parallel O_1D</math>, and <math>BC \parallel AD</math>
 +
 
 +
This means that <math>\Delta PDA \sim \Delta PBC \sim \Delta O_3O_1O_1</math>.  In other words, those three triangles are similar.
 +
 
 +
Since <math>r_1</math> is the circumcenter of <math>\Delta PDA</math>,
 +
 
 +
then <math>r_1=\frac{|AD| \times |DP| \times |AP|}{4A_1}=\frac{(3)(4)(6)}{4A_1}=\frac{18}{A_1}</math>
 +
 
 +
Let <math>h_1</math> be the height of <math>\Delta PDA</math> to side <math>AD</math>
 +
 
 +
Then, <math>A_1=\frac{|AD| \times h_1}{2}</math>, thus <math>h_1=\frac{2}{3}A_1</math>
 +
 
 +
Since <math>PR</math> is the height of <math>\Delta O_1O_2O_3</math> to side <math>O_1O_2</math>, then using similar triangles,
 +
 
 +
<math>\frac{|O_1O_2|}{|PR|}=\frac{|AD|}{h_1}</math>. Therefore, <math>\frac{r_1+r_2}{16}=\frac{3}{\frac{2}{3}A_1}</math>.  Solving for <math>r_2</math> we have:
 +
 
 +
<math>r_2=\frac{72}{A_1}-r_1=\frac{72}{A_1}-\frac{18}{A_1}=\frac{54}{A_1}=3\left( \frac{18}{A_1} \right)=3r_1</math>
 +
 
 +
By similar triangles,
 +
 
 +
<math>A_2=\left( \frac{r_2}{r_1} \right)^2A_1=9A_1</math>
 +
 
 +
Using Heron's formula,
 +
 
 +
<math>A_1=\sqrt{s(s-a)(s-b)(s-c)}</math>, where <math>s=\frac{a+b+c}{2}=\frac{3+6+4}{2}=\frac{13}{2}</math> we have:
 +
 
 +
<math>A_1=\sqrt{\left( \frac{13}{2} \right)\left( \frac{13}{2}-3\right)\left( \frac{13}{2}-6 \right)\left( \frac{13}{2}-4 \right)}</math>
 +
 
 +
<math>A_1=\frac{\sqrt{\left(13\right)\left(7\right)\left(1\right)\left(5\right)}}{4}=\frac{\sqrt{455}}{4}</math>
 +
 
 +
<math>A_2=9A_1=\frac{9\sqrt{455}}{4}=\frac{p\sqrt{q}}{r}</math>, thus <math>p=9,q=455,r=4</math>
 +
 
 +
<math>p+q+r=\boxed{468}</math>
 +
 
 +
~Tomas Diaz. orders@tomasdiaz.com
 +
 
 +
{{alternate solutions}}
 +
 
 +
==See Also==
 +
{{Mock AIME box|year=Pre 2005|n=3|num-b=13|num-a=15}}

Latest revision as of 01:05, 25 November 2023

Problem

Circles $\omega_1$ and $\omega_2$ are centered on opposite sides of line $l$, and are both tangent to $l$ at $P$. $\omega_3$ passes through $P$, intersecting $l$ again at $Q$. Let $A$ and $B$ be the intersections of $\omega_1$ and $\omega_3$, and $\omega_2$ and $\omega_3$ respectively. $AP$ and $BP$ are extended past $P$ and intersect $\omega_2$ and $\omega_1$ at $C$ and $D$ respectively. If $AD = 3, AP = 6, DP = 4,$ and $PQ = 32$, then the area of triangle $PBC$ can be expressed as $\frac{p\sqrt{q}}{r}$, where $p, q,$ and $r$ are positive integers such that $p$ and $r$ are coprime and $q$ is not divisible by the square of any prime. Determine $p + q + r$.

Solution

AIME 2005 14a.png

Let $O_1, O_2,$ and $O_3$ be the centers of $\omega_1, \omega_2$ and $\omega_3$ respectively.

Let point $R$ be the midpoint of $QP$. Thus, $O_3R \bot PQ$ and $|PR|=\frac{|PQ|}{2}=16$

Let $r_1$ and $r_2$ be the radii of circles $\omega_1$ and $\omega_2$ respectively.

Let $A_1$ and $A_2$ be the areas of triangles $PDA$ and $PBC$ respectively.

Since $O_3R \parallel O_1O_2$ and $\angle RO_3O_2 = \angle O_3O_2O_1$, then $O_2B \parallel O_1D$, and $BC \parallel AD$

This means that $\Delta PDA \sim \Delta PBC \sim \Delta O_3O_1O_1$. In other words, those three triangles are similar.

Since $r_1$ is the circumcenter of $\Delta PDA$,

then $r_1=\frac{|AD| \times |DP| \times |AP|}{4A_1}=\frac{(3)(4)(6)}{4A_1}=\frac{18}{A_1}$

Let $h_1$ be the height of $\Delta PDA$ to side $AD$

Then, $A_1=\frac{|AD| \times h_1}{2}$, thus $h_1=\frac{2}{3}A_1$

Since $PR$ is the height of $\Delta O_1O_2O_3$ to side $O_1O_2$, then using similar triangles,

$\frac{|O_1O_2|}{|PR|}=\frac{|AD|}{h_1}$. Therefore, $\frac{r_1+r_2}{16}=\frac{3}{\frac{2}{3}A_1}$. Solving for $r_2$ we have:

$r_2=\frac{72}{A_1}-r_1=\frac{72}{A_1}-\frac{18}{A_1}=\frac{54}{A_1}=3\left( \frac{18}{A_1} \right)=3r_1$

By similar triangles,

$A_2=\left( \frac{r_2}{r_1} \right)^2A_1=9A_1$

Using Heron's formula,

$A_1=\sqrt{s(s-a)(s-b)(s-c)}$, where $s=\frac{a+b+c}{2}=\frac{3+6+4}{2}=\frac{13}{2}$ we have:

$A_1=\sqrt{\left( \frac{13}{2} \right)\left( \frac{13}{2}-3\right)\left( \frac{13}{2}-6 \right)\left( \frac{13}{2}-4 \right)}$

$A_1=\frac{\sqrt{\left(13\right)\left(7\right)\left(1\right)\left(5\right)}}{4}=\frac{\sqrt{455}}{4}$

$A_2=9A_1=\frac{9\sqrt{455}}{4}=\frac{p\sqrt{q}}{r}$, thus $p=9,q=455,r=4$

$p+q+r=\boxed{468}$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See Also

Mock AIME 3 Pre 2005 (Problems, Source)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_3_Pre_2005_Problems/Problem_14&oldid=205688"