Difference between revisions of "2007 AMC 10B Problems/Problem 21"

Latest revision as of 15:52, 29 July 2024

Problem

Right $\triangle ABC$ has $AB=3, BC=4,$ and $AC=5.$ Square $XYZW$ is inscribed in $\triangle ABC$ with $X$ and $Y$ on $\overline{AC}, W$ on $\overline{AB},$ and $Z$ on $\overline{BC}.$ What is the side length of the square?

$\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2$

Solution 1

There are lots of similar triangles in the diagram, but we will only use $\triangle WBZ \sim \triangle ABC.$ If $h$ is the altitude from $B$ to $AC$ and $s$ is the sidelength of the square, then $h-s$ is the altitude from $B$ to $WZ.$ By similar triangles, $\begin{align*} \frac{h-s}{h}&=\frac{s}{5}\\ 5(h-s)&=hs\\ 5h-5s&=hs\\ 5h&=s(h+5)\\ s&=\frac{5h}{h+5} \end{align*}$

Find the length of the altitude of $\triangle ABC.$ Since it is a right triangle, the area of $\triangle ABC$ is $\frac{1}{2}(3)(4) = 6.$

The area can also be expressed as $\frac{1}{2}(5)(h),$ so $\frac{5}{2}h=6 \longrightarrow h=2.4.$

Substitute back into $s.$

$s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}$

Solution 2

Let $l$ be the side length of the inscribed square. Note that $\triangle ZYC \sim \triangle WBZ \sim \triangle ABC$ .

Then we can setup the following ratios:

$\frac{CZ}{l} = \frac{5}{3} \rightarrow CZ = \frac{5}{3}l$ $\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l$

But then $\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}$

Video Solution by OmegaLearn

https://youtu.be/FDgcLW4frg8?t=4662

~ pi_is_3.14

@@ Line 5: / Line 5: @@
 <math>\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2 </math>
-==Solution==
+==Solution 1==
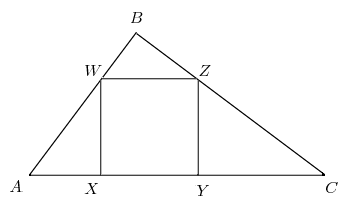
 [[Image:2007AMC10B21.png|center]]
-There are many similar triangles in the diagram, but we will only be using <math>\triangle WBZ \sim \triangle ABC.</math> If <math>h</math> is the altitude from <math>B</math> to <math>AC</math> and <math>s</math> is the sidelength of the square, then <math>h-s</math> is the altitude from <math>B</math> to <math>WZ.</math> By similar triangles,
+There are lots of similar triangles in the diagram, but we will only use <math>\triangle WBZ \sim \triangle ABC.</math> If <math>h</math> is the altitude from <math>B</math> to <math>AC</math> and <math>s</math> is the sidelength of the square, then <math>h-s</math> is the altitude from <math>B</math> to <math>WZ.</math> By similar triangles,
 <cmath>\begin{align*}
-\frac{h-s}{s}&=\frac{h}{5}\\
+\frac{h-s}{h}&=\frac{s}{5}\\
+(h-s)&=hs\\
 h-5s&=hs\\
 h&=s(h+5)\\
@@ Line 24: / Line 25: @@
 <cmath>s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}</cmath>
+==Solution 2==
+Let <math>l</math> be the side length of the inscribed square. Note that <math>\triangle ZYC \sim \triangle WBZ \sim \triangle ABC</math>.
+Then we can setup the following ratios:
+<cmath>\frac{CZ}{l} = \frac{5}{3} \rightarrow CZ = \frac{5}{3}l</cmath>
+<cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath>
+But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}</math>
+== Video Solution by OmegaLearn==
+https://youtu.be/FDgcLW4frg8?t=4662
+~ pi_is_3.14
 ==See Also==

2007 AMC 10B (Problems • Answer Key • Resources)
Preceded by Problem 20	Followed by Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search