Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1973 IMO Problems/Problem 2"

m
 
(37 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
Determine whether or not there exists a finite set M of points in space not
+
==Problem==
−
lying in the same plane such that, for any two points A and B of M; one can
+
Determine whether or not there exists a finite set <math>M</math> of points in space not lying in the same plane such that, for any two points <math>A</math> and <math>B</math> of <math>M</math>; one can select two other points <math>C</math> and <math>D</math> of <math>M</math> so that lines <math>AB</math> and <math>CD</math> are parallel and not coincident.
−
select two other points C and D of M so that lines AB and CD are parallel
+
 
−
and not coincident.
+
==Solution==
−
{{solution}}
+
 
 +
In order to solve this problem we can start by finding at least one finite set <math>M</math> that satisfies the condition.
 +
 
 +
We start by defining our first set <math>M_{8}</math> with the vertices of a cube of side <math>k</math> as follows:
 +
<math>M_{8} = \{ (0,0,0), (k,0,0), (k,k,0), (0,k,0), (0,0,k), (k,0,k), (k,k,k), (0,k,k) \}</math> 
 +
 
 +
Since all the faces of this cube have a parallel face, then any two points on one face will have corresponding 2 points on the opposite face that is parallel.  However we have four diagonals on this cube that do not have two points that are parallel to any of these diagonals.
 +
 
 +
By doing a reflection of the points on the <math>z=k</math> plane along the <math>xy</math>-plane these four diagonals will have their respective parallel diagonals on the <math>z \le 0</math> space.
 +
 
 +
But now we have four more diagonals on the set of two cubes that do not have a parallel line.  That is, diagonal <math>(0,0,-k) \rightarrow (k,k,k)</math> does not have a parallel line and neither do the other three.
 +
 
 +
By doing a reflection of the points on the <math>x=k</math> plane along the <math>yz</math>-plane these new four diagonals will have their respective parallel diagonals on the <math>x \le 0</math> space.
 +
 
 +
But now we have four more diagonals on the set of 4 cubes that do not have a parallel line.  That is, diagonal <math>(-k,0,-k) \rightarrow (k,k,k)</math> does not have a parallel line and neither do the other three.
 +
 
 +
By doing a reflection of the points on the <math>y=k</math> plane along the <math>xz</math>-plane these new four diagonals will have their respective parallel diagonals on the <math>y \le 0</math> space.
 +
 
 +
The new 4 longer diagonals will cross the diagonal of two of the cubes and will have a parallel line on one of the other cubes.
 +
 
 +
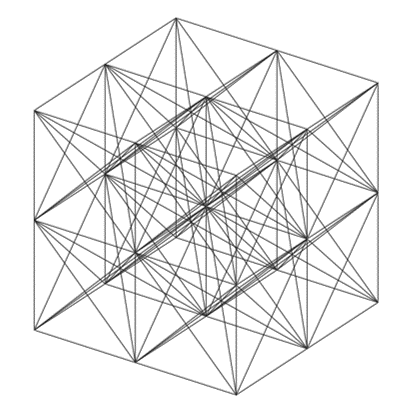
So, we found a set at least one finite set <math>M</math> that we can define as <math>M=\{(x,y,z)\}</math> where <math>x,y,z \in \{-k,0,k\}</math> giving a total of 27 points.  Therefore such a set exists.
 +
 
 +
Another way to define this set of points is let <math>M</math> be:
 +
 
 +
Let <math>V</math> be a solid cube or right angled parallelepiped
 +
 
 +
Let <math>M_{v}</math> be the set of all 8 vertices of <math>V</math>
 +
 
 +
Let <math>M_{me}</math> be the set of all 12 midpoints of the edges of <math>V</math>
 +
 
 +
Let <math>M_{mf}</math> be the set of all 6 midpoints of the faces of <math>V</math>
 +
 
 +
Let <math>M_{c}</math> be the center of <math>V</math>
 +
 
 +
<math>M</math>=<math>M_{v} \cup M_{me} \cup M_{mf} \cup M_{c}</math>
 +
 
 +
It is possible that one can construct many other sets of <math>M</math> using regular tetrahedrons with some reflections and with less points than 27, or by translating or rotating or skewing all the the points simultaneously of the finite set <math>M</math> that we defined here.  But that is not necessary for this problem because it asks to prove whether there exist a set with the described conditions.  By showing that at least one set exists with those conditions, the problem is proved.
 +
 
 +
[[File:IMO_1973_P2_01.png]]
 +
 
 +
~Tomas Diaz.  orders@tomasdiaz.com
 +
 
 +
{{alternate solutions}}
 +
 
 +
== See Also == {{IMO box|year=1973|num-b=1|num-a=3}}
 
[[Category:Olympiad Geometry Problems]]
 
[[Category:Olympiad Geometry Problems]]
 
[[Category:3D Geometry Problems]]
 
[[Category:3D Geometry Problems]]

Latest revision as of 20:33, 21 November 2023

Problem

Determine whether or not there exists a finite set $M$ of points in space not lying in the same plane such that, for any two points $A$ and $B$ of $M$; one can select two other points $C$ and $D$ of $M$ so that lines $AB$ and $CD$ are parallel and not coincident.

Solution

In order to solve this problem we can start by finding at least one finite set $M$ that satisfies the condition.

We start by defining our first set $M_{8}$ with the vertices of a cube of side $k$ as follows: $M_{8} = \{ (0,0,0), (k,0,0), (k,k,0), (0,k,0), (0,0,k), (k,0,k), (k,k,k), (0,k,k) \}$

Since all the faces of this cube have a parallel face, then any two points on one face will have corresponding 2 points on the opposite face that is parallel. However we have four diagonals on this cube that do not have two points that are parallel to any of these diagonals.

By doing a reflection of the points on the $z=k$ plane along the $xy$-plane these four diagonals will have their respective parallel diagonals on the $z \le 0$ space.

But now we have four more diagonals on the set of two cubes that do not have a parallel line. That is, diagonal $(0,0,-k) \rightarrow (k,k,k)$ does not have a parallel line and neither do the other three.

By doing a reflection of the points on the $x=k$ plane along the $yz$-plane these new four diagonals will have their respective parallel diagonals on the $x \le 0$ space.

But now we have four more diagonals on the set of 4 cubes that do not have a parallel line. That is, diagonal $(-k,0,-k) \rightarrow (k,k,k)$ does not have a parallel line and neither do the other three.

By doing a reflection of the points on the $y=k$ plane along the $xz$-plane these new four diagonals will have their respective parallel diagonals on the $y \le 0$ space.

The new 4 longer diagonals will cross the diagonal of two of the cubes and will have a parallel line on one of the other cubes.

So, we found a set at least one finite set $M$ that we can define as $M=\{(x,y,z)\}$ where $x,y,z \in \{-k,0,k\}$ giving a total of 27 points. Therefore such a set exists.

Another way to define this set of points is let $M$ be:

Let $V$ be a solid cube or right angled parallelepiped

Let $M_{v}$ be the set of all 8 vertices of $V$

Let $M_{me}$ be the set of all 12 midpoints of the edges of $V$

Let $M_{mf}$ be the set of all 6 midpoints of the faces of $V$

Let $M_{c}$ be the center of $V$

$M$=$M_{v} \cup M_{me} \cup M_{mf} \cup M_{c}$

It is possible that one can construct many other sets of $M$ using regular tetrahedrons with some reflections and with less points than 27, or by translating or rotating or skewing all the the points simultaneously of the finite set $M$ that we defined here. But that is not necessary for this problem because it asks to prove whether there exist a set with the described conditions. By showing that at least one set exists with those conditions, the problem is proved.

IMO 1973 P2 01.png

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See Also

1973 IMO (Problems) • Resources
Preceded by
Problem 1 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 3
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1973_IMO_Problems/Problem_2&oldid=205187"