Difference between revisions of "2011 AIME II Problems/Problem 8"

Revision as of 14:36, 2 June 2020

Problem

Let $z_1,z_2,z_3,\dots,z_{12}$ be the 12 zeroes of the polynomial $z^{12}-2^{36}$ . For each $j$ , let $w_j$ be one of $z_j$ or $i z_j$ . Then the maximum possible value of the real part of $\displaystyle\sum_{j=1}^{12} w_j$ can be written as $m+\sqrt{n}$ where $m$ and $n$ are positive integers. Find $m+n$ .

Solution

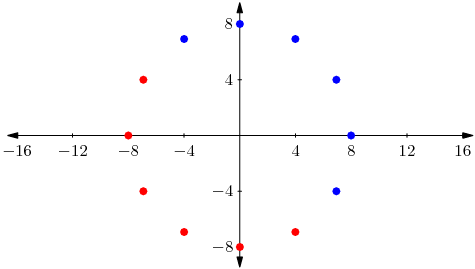
The twelve dots above represent the $12$ roots of the equation $z^{12}-2^{36}=0$ . If we write $z=a+bi$ , then the real part of $z$ is $a$ and the real part of $iz$ is $-b$ . The blue dots represent those roots $z$ for which the real part of $z$ is greater than the real part of $iz$ , and the red dots represent those roots $z$ for which the real part of $iz$ is greater than the real part of $z$ . Now, the sum of the real parts of the blue dots is easily seen to be $8+16\cos\frac{\pi}{6}=8+8\sqrt{3}$ and the negative of the sum of the imaginary parts of the red dots is easily seen to also be $8+8\sqrt{3}$ . Hence our desired sum is $16+16\sqrt{3}=16+\sqrt{768}$ , giving the answer $\boxed{784}$ .

Solution 2

The equation $z^{12}-2^{36}=0$ can be factored as follows: $(z^6-2^{18})(z^6+2^{18})=0$ $(z^2-2^6)(z^2+2^6)({(z^2+2^6)}^2-z^2\cdot2^6)({(z^2-2^6)}^2+z^2\cdot2^6)=0$ $(z^2-2^6)(z^2+2^6)(z^2+2^6-z\cdot2^3)(z^2+2^6+z\cdot2^3) (z^2-2^6-iz\cdot2^3)(z^2-2^6+i z\cdot2^3)=0$

Since this is a 12th degree equation, there are 12 roots. Also, since each term in the equation is even, the positive or negative value of each root is another root. That would mean there are 6 roots that can be multiplied by $-1$ and since we have 6 factors, that’s 1 root per factor. We just need to solve for $z$ in each factor and pick whether or not to multiply by $i$ and $-1$ for each one depending on the one that yields the highest real value. After that process, we get $8+8+2((4\sqrt{3}+4)+(4\sqrt{3}-4))$ Adding the values up yields $16+16\sqrt{3}$ , or $16+\sqrt{768}$ , and $16+768=\boxed{784}$ .

-Solution by Someonenumber011.

Solution 3

Using the diagram from solution 1, note that multiplying by $i$ is rotating counterclockwise by $\frac{\pi}{2}$ . From there, we eventually get $16+768=\boxed{784}$ . ~Lcz

@@ Line 21: / Line 21: @@
 ==Solution 3==
 Using the diagram from solution 1, note that multiplying by <math>i</math> is rotating counterclockwise by <math>\frac{\pi}{2}</math>. From there, we eventually get <math>16+768=\boxed{784}</math>.
+~Lcz
 ==See also==

2011 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 7	Followed by Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search