Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 14"
m |
|||
| Line 35: | Line 35: | ||
== Problem Source == | == Problem Source == | ||
| − | 4everwise thought of this problem after reading the first chapter of Geometry Revisited. | + | 4everwise thought of this problem after reading the first chapter of [http://www.amazon.com/exec/obidos/ASIN/0883856190/artofproblems-20 Geometry Revisited]. |
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
Revision as of 17:18, 15 February 2007
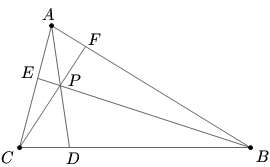
Problem
In triangle 
, 
and 
. Given that 
, 
and 
intersect at 
and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of 
Solution
Let 
.
By the Angle Bisector Theorem, 
.
Let 
. Then by the Pythagorean Theorem, 
and 
. Subtracting the former equation from the latter to eliminate 
, we have 
so 
. Since 
, 
. We can solve these equations for 
and 
in terms of 
to find that 
and 
.
Now, by Ceva's Theorem, 
, so 
and 
. Plugging in the values we previously found,
so
and
which yields finally 
.
Problem Source
4everwise thought of this problem after reading the first chapter of Geometry Revisited.
