Difference between revisions of "Two poles formula"

Latest revision as of 18:31, 17 August 2021

Theorem

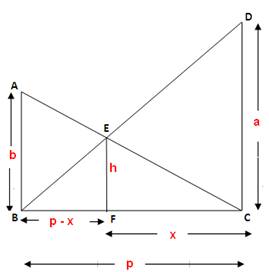
The two pole formula/theorem states that for two poles some distance apart, the height of the intersection point of the lines joining the top of either pole to the foot of the opposite pole is half the harmonic mean of the heights of the two poles(and that this is true regardless of the distance between the two poles).

Proof using similar triangles

We are looking to show that for the two poles $\overline{AB}$ and $\overline{CD}$ of heights $a$ and $b$ , respectively, and $p$ units apart, $h=\frac{1}{2}\cdot\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{ab}{a+b}$ .

Because $\triangle{ECF} \sim \triangle{ACB}$ , $\frac{h}{x}=\frac{b}{p}$ $x=\frac{hp}{b}.$ Because $\triangle{EBF} \sim \triangle{DBC}$ , $\frac{h}{p-x}=\frac{a}{p}$ $hp=ap-ax$ $x=\frac{ap-hp}{a}.$ Therefore, $\frac{hp}{b}=\frac{ap-hp}{a}$ $ahp=abp-bhp$ $ahp+bhp=abp$ $hp(a+b)=abp$ $h=\frac{ab}{a+b},$ as desired.

$Q.E.D.$ $\smiley$

Coordinate/analytical geometry proof

Using the same diagram as above, if we let $B$ be the origin, then $A,C,$ and $D$ are the points $(0,b),(p,0)$ and $(p,a),$ respectively. Hence, $\overline{AC}$ and $\overline{BD}$ have slopes of $\frac{b-0}{0-p}=-\frac{b}{p}$ and $\frac{a-0}{p-0}=\frac{a}{p}$ , respectively, and y-intercepts of $(0,b)$ and $(0,0)$ , respectively. That means their equations are $y=-\frac{b}{p}x+b$ and $y=\frac{a}{p}x$ , respectively. Setting the two equations equal to find the intersection point(recall that a point is shared by two lines if and only if it satisfies the equation of both lines), we obtain $-\frac{b}{p}x+b=\frac{a}{p}x$ $\frac{b}{p}x+\frac{a}{p}x=b$ $(\frac{a+b}{p})x=b$ $x=\frac{b}{\frac{a+b}{p}}$ $x=\frac{bp}{a+b}.$ To find the ordinate, we plug in this to either equation of $\overline{AC}$ or $\overline{BD}$ (in this case, we choose $\overline{BD}$ 's equation because it contains fewer terms): $y=\frac{a}{p}x=\frac{a}{p} \cdot \frac{bp}{a+b}$ $y=\frac{abp}{p(a+b)}$ $y=\frac{ab}{a+b},$ so $E$ is the ordered pair $(\frac{bp}{a+b},\frac{ab}{a+b})$ . Therefore, the height is $\frac{ab}{a+b}$ , as desired. $Q.E.D.$ $\smiley$

Image Credit

https://images.app.goo.gl/237wxi3A4qAEWNFW8

@@ Line 34: / Line 34: @@
 <cmath>x=\frac{b}{\frac{a+b}{p}}</cmath>
 <cmath>x=\frac{bp}{a+b}.</cmath>
-To find the ordinate, we plug in this to either equation of <math>\overline{AC}</math> or <math>\overline{BD}</math>(in this case, we choose <math>\overline{AC}</math>'s equation because it contains fewer terms):
+To find the ordinate, we plug in this to either equation of <math>\overline{AC}</math> or <math>\overline{BD}</math>(in this case, we choose <math>\overline{BD}</math>'s equation because it contains fewer terms):
 <cmath>y=\frac{a}{p}x=\frac{a}{p} \cdot \frac{bp}{a+b}</cmath>
 <cmath>y=\frac{abp}{p(a+b)}</cmath>

Page

Toolbox

Search