Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "British Mathematical Olympiad"

(→‎21-th Mathematical Olympiad 1985 Problem 5)
(→‎Solution)
Line 16: Line 16:
 
In a right circular cone the semi-vertical angle of which is <math>\theta</math>, a cube is placed so that four of its vertices are on the base and four on the curved surface. Prove that as <math>\theta</math> varies the maximum value of the ratio of the volume of the cube to the volume of the cone occurs when <math>3\sin \theta = 1.</math>
 
In a right circular cone the semi-vertical angle of which is <math>\theta</math>, a cube is placed so that four of its vertices are on the base and four on the curved surface. Prove that as <math>\theta</math> varies the maximum value of the ratio of the volume of the cube to the volume of the cone occurs when <math>3\sin \theta = 1.</math>
 
===Solution===
 
===Solution===
−
[[File:British 1985 3D.png|350px|right]]
+
[[File:Ron Cone Cube D.png|400px|right]]
−
 
+
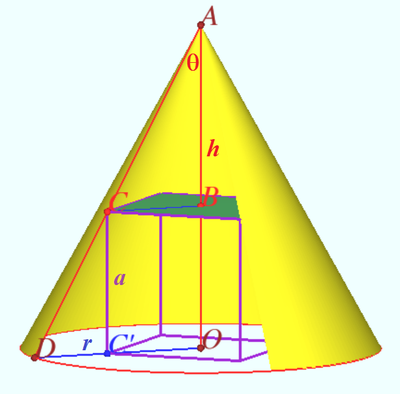
Let the cube side be <math>a,</math> height of the cone be <math>h,</math> radius of the cone be <math>r = h \tan \theta.</math>
 +
Notation is shown on diagram. <math>A</math> is the vertex of the cone, <math>B</math> is the center of the cube upper face, <math>C</math> is the vertex of upper surface of the cube, <math>O</math> is the center of the base of the cone, <math>D</math> is the point where <math>AC</math> cross the base of the cone.
 +
<cmath>BO = a, BC = \frac {a}{\sqrt {2}}, AO = h, DO = r = h \tan \theta.</cmath>
 +
<cmath>\frac {AB}{AO} = \frac {BC}{OD} \implies \frac {h-a}{h} = \frac {a}{r \sqrt{2}} \implies \frac{r}{a} = \tan \theta + \frac {1}{\sqrt{2}}.</cmath>
 +
The ratio of the volume of the cube to the volume of the cone is
 +
<cmath>\bar V = \frac {3a^3}{\pi r^2 h} = \frac {3r}{\pi h} \cdot \left( \frac {a}{r} \right)^3 = \frac {3}{\pi} \cdot \frac {\tan \theta}{(\tan \theta + \frac {1}{\sqrt{2}})^3} = \frac {3}{\pi f^3}.</cmath>
 +
Denote <cmath>x^3 = \tan \theta, f = \frac {x^3 + \frac {1}{\sqrt{2}} }{x} = x^2 + \frac {1}{x \sqrt {2}} = x^2 +  \frac {1}{2x \sqrt {2}} +  \frac {1}{2x \sqrt {2}},</cmath>
 +
<cmath>f \ge 3 \sqrt [3] {x^2 \cdot \frac {1}{2x \sqrt {2}} \cdot \frac {1}{2x \sqrt {2}}} = \frac {3}{2}</cmath> if
 +
<cmath>x^2 = \frac {1}{2x \sqrt {2}} \implies  \tan \theta = x^3 = \frac {1}{2 \sqrt {2}} \implies \sin \theta = \frac {1}{3}.</cmath>
 +
<cmath> \bar V = \frac {3}{\pi f^3} \ge \frac {8}{9 \pi} = 0.283.</cmath>
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
  

Revision as of 16:00, 5 June 2023

The British Mathematical Olympiad is a national math competition held in the United Kingdom. Solvers who score over a certain threshold in the Senior Mathematical Challenge are automatically entered to the first round, but others can register for the first round.

Structure

The British Mathematical Olympiad is divided into two rounds. In the first round (BMO 1), solvers have 3.5 hours to solve 6 problems. High scorers can move on into the second round (BMO 2), where solvers have 3.5 hours to solve 4 problems.

For both rounds, each problem is worth 10 points. Like most Olympiads, complete solutions are required in order to get full credit.

Participants who submit a solution with the highest quality in BMO 2 can earn the Christopher Bradley elegance prize.

Resources

8-th British Mathematical Olympiad 1972 Problem 5

In a right circular cone the semi-vertical angle of which is $\theta$, a cube is placed so that four of its vertices are on the base and four on the curved surface. Prove that as $\theta$ varies the maximum value of the ratio of the volume of the cube to the volume of the cone occurs when $3\sin \theta = 1.$

Solution

Ron Cone Cube D.png

Let the cube side be $a,$ height of the cone be $h,$ radius of the cone be $r = h \tan \theta.$ Notation is shown on diagram. $A$ is the vertex of the cone, $B$ is the center of the cube upper face, $C$ is the vertex of upper surface of the cube, $O$ is the center of the base of the cone, $D$ is the point where $AC$ cross the base of the cone. \[BO = a, BC = \frac {a}{\sqrt {2}}, AO = h, DO = r = h \tan \theta.\] \[\frac {AB}{AO} = \frac {BC}{OD} \implies \frac {h-a}{h} = \frac {a}{r \sqrt{2}} \implies \frac{r}{a} = \tan \theta + \frac {1}{\sqrt{2}}.\] The ratio of the volume of the cube to the volume of the cone is \[\bar V = \frac {3a^3}{\pi r^2 h} = \frac {3r}{\pi h} \cdot \left( \frac {a}{r} \right)^3 = \frac {3}{\pi} \cdot \frac {\tan \theta}{(\tan \theta + \frac {1}{\sqrt{2}})^3} = \frac {3}{\pi f^3}.\] Denote \[x^3 = \tan \theta, f = \frac {x^3 + \frac {1}{\sqrt{2}} }{x} = x^2 + \frac {1}{x \sqrt {2}} = x^2 + \frac {1}{2x \sqrt {2}} + \frac {1}{2x \sqrt {2}},\] \[f \ge 3 \sqrt [3] {x^2 \cdot \frac {1}{2x \sqrt {2}} \cdot \frac {1}{2x \sqrt {2}}} = \frac {3}{2}\] if \[x^2 = \frac {1}{2x \sqrt {2}} \implies \tan \theta = x^3 = \frac {1}{2 \sqrt {2}} \implies \sin \theta = \frac {1}{3}.\] \[\bar V = \frac {3}{\pi f^3} \ge \frac {8}{9 \pi} = 0.283.\] vladimir.shelomovskii@gmail.com, vvsss

21-th Mathematical Olympiad 1985 Problem 5

A circular hoop of radius 4 cm is held fixed in a horizontal plane. A cylinder with radius 4 cm and length 6 cm rests on the hoop with its axis horizontal, and with each of its two circular ends touching the hoop at two points. The cylinder is free to move subject to the condition that each of its circular ends always touches the hoop at two points. Find, with proof, the locus of the centre of one of the cylinder’s circular ends.

Solution

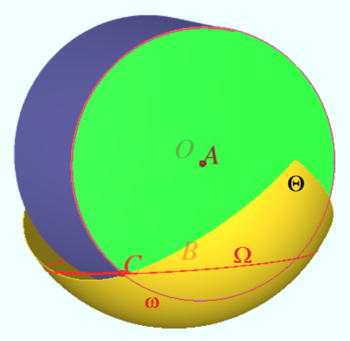
British 1985 3D.png

Let the centroid of the cylinder be the point $O.$ The side surface of the cylinder is shown by dark blue.

Let the center of one of the circular ends be the point $A.$ This end is shown by green. Its edge is a purple circle $\omega, OA = 3.$

Let the center of the hoop $\Omega$ be $B.$ The hoop is shown by red.

Let $\omega$ cross $\Omega$ at point $C.$ Therefore $\omega$ cross $\Omega$ at second point symmetrical to $C$ with respect to the plane $OAB.$ \[AC = BC = 4, BC \perp OA \implies AC = 5.\] Let $\Theta$ be the sphere of radius $5$ centered at $O.$ Part of this sphere is shown in the diagram by yellow. Let the cylinder is glued to the sphere and point $O$ is fixed.

In this case $\omega$ and $\Omega$ both lie on $S,$ and point $A$ lies on the sphere centered at $O$ with radius $OA = 3.$

The clime “The cylinder is free to move subject to the condition that each of its circular ends always touches the hoop at two points” has the equivalent form “The sphere is free to move with fixed center subject to the condition that $\omega$ cross $\Omega.$”

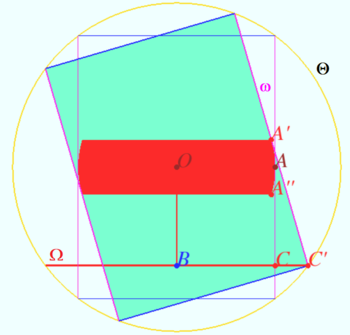
If the sphere rotates around an axis $OB,$ then point $A$ moves along circle with axis $OB.$

British 1985.png

Let the sphere rotates around an axis perpendicular $OA$ and $OB.$ Axis view is shown on the diagram. We rotate $\Theta$ together with $\omega$ in counterclockwise direction. Point $C$ moves along $\Omega$ till point $C'$ in the plane $OAB$ where $\omega$ touch $\Omega.$ The point $A$ moves to extreme position $A'.$

If one rotate $\Theta$ in clockwise direction, point $A$ moves to position $A''$ symmetric to $A'$ with respect $OA.$ \[OA = OB = 3, BC' = A'C'= 4,\] \[\angle A'C'B = 2 \arcsin \frac {3}{5} \implies\] \[A'A'' = 2(\frac {96}{25} - 3) = \frac {42}{25} = 1.68.\] The locus of the point $A$ is the belt with a width of $1.68$ cm located on a sphere with a radius of $3$ cm symmetrically to the circumference of the great circle located parallel hoop.

vladimir.shelomovskii@gmail.com, vvsss

Comments

This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=British_Mathematical_Olympiad&oldid=193928"