Difference between revisions of "2021 AIME I Problems/Problem 6"
Boppitybop (talk | contribs) m (→Solution 2 (Solution 1 with Slight Simplification)) |
m (→Solution 3) |
||
| Line 36: | Line 36: | ||
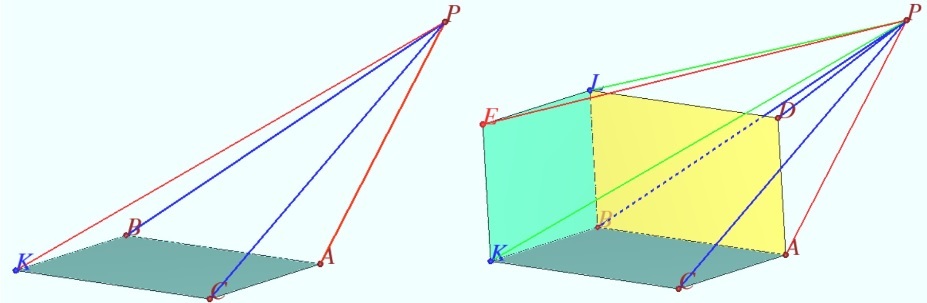
Let <math>E</math> be the vertex of the cube such that <math>ABED</math> is a square. | Let <math>E</math> be the vertex of the cube such that <math>ABED</math> is a square. | ||
| − | + | Using the [[British Flag Theorem]], we can easily show that | |
<cmath>PA^2 + PE^2 = PB^2 + PD^2</cmath> | <cmath>PA^2 + PE^2 = PB^2 + PD^2</cmath> | ||
and | and | ||
Revision as of 00:09, 3 December 2023
Contents
Problem
Segments ![]() and
and ![]() are edges of a cube and
are edges of a cube and ![]() is a diagonal through the center of the cube. Point
is a diagonal through the center of the cube. Point ![]() satisfies
satisfies ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]()
Solution 1
First scale down the whole cube by ![]() . Let point
. Let point ![]() have coordinates
have coordinates ![]() , point
, point ![]() have coordinates
have coordinates ![]() , and
, and ![]() be the side length. Then we have the equations
be the side length. Then we have the equations
 These simplify into
These simplify into
 Adding the first three equations together, we get
Adding the first three equations together, we get ![]() .
Subtracting this from the fourth equation, we get
.
Subtracting this from the fourth equation, we get ![]() , so
, so ![]() . This means
. This means ![]() . However, we scaled down everything by
. However, we scaled down everything by ![]() so our answer is
so our answer is ![]() .
.
~JHawk0224
Solution 2 (Solution 1 with Slight Simplification)
Once the equations for the distance between point P and the vertices of the cube have been written, we can add the first, second, and third to receive, ![]() Subtracting the fourth equation gives
Subtracting the fourth equation gives
 Since point
Since point ![]() , and since we scaled the answer is
, and since we scaled the answer is ![]() .
.
~Aaryabhatta1
Solution 3
Let ![]() be the vertex of the cube such that
be the vertex of the cube such that ![]() is a square.
Using the British Flag Theorem, we can easily show that
is a square.
Using the British Flag Theorem, we can easily show that
![]() and
and
![]() Hence, by adding the two equations together, we get
Hence, by adding the two equations together, we get ![]() . Substituting in the values we know, we get
. Substituting in the values we know, we get ![]() .
.
Thus, we can solve for ![]() , which ends up being
, which ends up being ![]() .
.
Solution 4
For all points ![]() in space, define the function
in space, define the function ![]() by
by ![]() . Then
. Then ![]() is linear; let
is linear; let ![]() be the center of
be the center of ![]() . Then since
. Then since ![]() is linear,
is linear,
 where
where ![]() denotes the side length of the cube. Thus
denotes the side length of the cube. Thus

Video Solution by Punxsutawney Phil
https://youtube.com/watch?v=vaRfI0l4s_8
See Also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.