Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Surface of constant width"

(→‎Rotation of the Reuleaux triangle)
(→‎Rotation of the Reuleaux triangle analogue)
Line 51: Line 51:
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Meissner solids==
 +
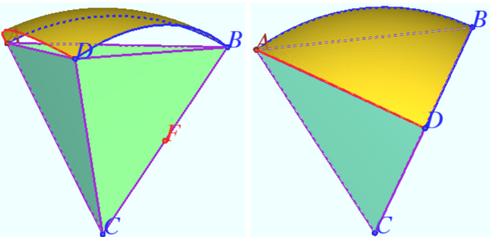
[[File:Sail two views.png|490px|right]]
 +
Let <math>ABCD</math> be the regular tetrahedron.
 +
 +
The «sail» <math>ABD</math> is the piece of sphere centered at the vertex <math>C</math> with radii <math>AB = AC</math> bounded by the planes <math>ACD, BCD,</math> and <math>ADF,</math> where <math>F</math> is the mipoint of <math>BC.</math>
 +
 +
The view along line <math>DF</math> is shown at the left part of diagram.
 +
 +
Let point <math>E \in  \overset{\Large\frown} {AD}</math> be the center of arc  <math>\overset{\Large\frown} {BC}</math> with radii <math>CE = BE = AB</math> shown by red.
 +
 +
The set of such arcs centered at points lying on the arc <math>\overset{\Large\frown} {AD}</math> create a part of lemon-shaped solid between arc <math>\overset{\Large\frown} {BC}</math> of the plane <math>BCD</math> and arc <math>\overset{\Large\frown} {BC}</math> of the plane <math>BCA,</math> shown at right part of diagram.

Revision as of 12:54, 10 August 2024

A curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. A surface of constant width (orbiform) is a convex form whose width, measured by the distance between two opposite parallel planes touching its boundary, is the same regardless of the direction of those two parallel planes.

Reuleaux triangle

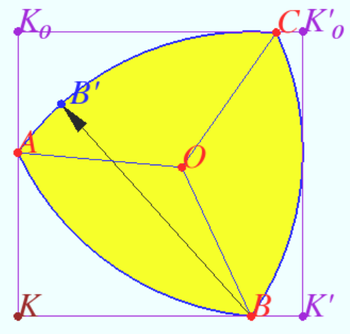
Reuleaux triangle.png

The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle.

Let $\triangle ABC$ be equilateral triangle.

Let $\overset{\Large\frown} {AC}$ be the arc centered at $B$ with radius $BB' = BA, \angle ABC = 60^\circ.$

Arcs $\overset{\Large\frown} {AB}$ and $\overset{\Large\frown} {BC}$ define similarly.

All points on this arcs are equidistant from the opposite vertex.

Distance is $|AB|.$

vladimir.shelomovskii@gmail.com, vvsss

Reuleaux triangle analogue

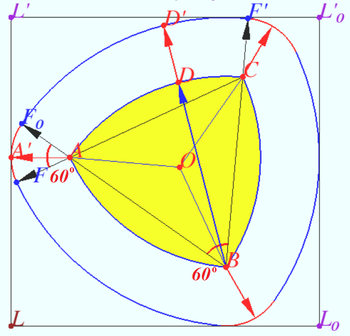
Reuleaux triangle analogue.png

Let $ABCD$ be the boundary of a Reuleaux triangle, $O$ be the centroid of $\triangle ABC.$

Let $\overset{\Large\frown} {FF_0}$ be the arc centered at $A$ with radius $AA', \angle FAF_0 = 60^\circ,$ points $F, A, C$ and $F_0, A, B$ are collinear.

Let $\overset{\Large\frown} {F_0F'}$ be the arc centered at $B$ with radius \[|AA'| + |AB|,\] $\angle F'AF_0 = \angle ABC = 60^\circ,$ points $F', C, B$ are collinear.

Similarly define arcs from point $F'$ to $F.$

The width of this curve is \[|AB| + 2|AA'|.\]

vladimir.shelomovskii@gmail.com, vvsss

Rotation of the Reuleaux triangle

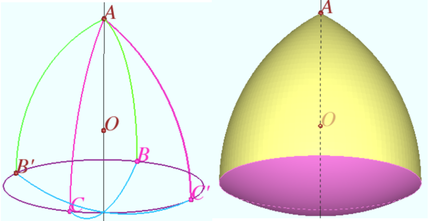
Solid Reuleaux triangle rotation.png

The left part of diagram shows the curve $ABC$ which is a Reuleaux triangle determined by the center $O$ and the vertex $A.$

The Reuleaux triangle $AB'C'$ is constructed by the rotation of the curve $ABC$ around axis $AO.$

The right part of the diagram shows the surface which arose as the result of the rotation $ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Rotation of the Reuleaux triangle analogue

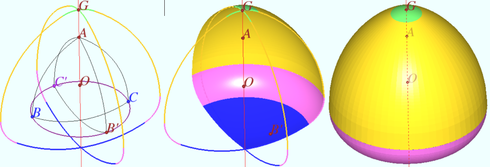
Surface Reuleaux triangle analogy construction.png

The left part of diagram shows the curve $G$ which is a Reuleaux triangle analogy determined by the center $O,$ the vertex $A$ and point $G$ on curve analogue.

Similarly, we use the Reuleaux triangle $AB'C'$ is constructed by the rotation of the curve $G$ around axis $AO$ and get the second position of the Reuleaux triangle analogue.

The middle part of the diagram shows part of the surface. We can see all four parts of this surface shown by different colors.

The right part of the diagram shows the surface which arose as the result of the rotation curve $G.$ It is impossible see the down side of the surface (blue) in this view.

vladimir.shelomovskii@gmail.com, vvsss

Meissner solids

Sail two views.png

Let $ABCD$ be the regular tetrahedron.

The «sail» $ABD$ is the piece of sphere centered at the vertex $C$ with radii $AB = AC$ bounded by the planes $ACD, BCD,$ and $ADF,$ where $F$ is the mipoint of $BC.$

The view along line $DF$ is shown at the left part of diagram.

Let point $E \in \overset{\Large\frown} {AD}$ be the center of arc $\overset{\Large\frown} {BC}$ with radii $CE = BE = AB$ shown by red.

The set of such arcs centered at points lying on the arc $\overset{\Large\frown} {AD}$ create a part of lemon-shaped solid between arc $\overset{\Large\frown} {BC}$ of the plane $BCD$ and arc $\overset{\Large\frown} {BC}$ of the plane $BCA,$ shown at right part of diagram.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Surface_of_constant_width&oldid=224879"