Difference between revisions of "1989 AIME Problems/Problem 15"
m |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
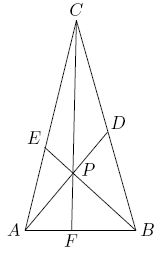
| + | Point <math>P^{}_{}</math> is inside <math>\triangle ABC^{}_{}</math>. Line segments <math>APD^{}_{}</math>, <math>BPE^{}_{}</math>, and <math>CPF^{}_{}</math> are drawn with <math>D^{}_{}</math> on <math>BC^{}_{}</math>, <math>E^{}_{}</math> on <math>AC^{}_{}</math>, and <math>F{}{}^{}_{}</math> on <math>AB^{}_{}</math> (see the figure at right). Given that <math>AP=6^{}_{}</math>, <math>BP=9^{}_{}</math>, <math>PD=6^{}_{}</math>, <math>PE=3^{}_{}</math>, and <math>CF=20^{}_{}</math>, find the area of <math>\triangle ABC^{}_{}</math>. | ||
| + | |||
| + | [[Image:AIME_1989_Problem_15.png]] | ||
== Solution == | == Solution == | ||
| + | {{solution}} | ||
== See also == | == See also == | ||
| + | * [[1989 AIME Problems/Problem 14|Previous Problem]] | ||
* [[1989 AIME Problems]] | * [[1989 AIME Problems]] | ||
Revision as of 22:29, 24 February 2007
Problem
Point 
is inside 
. Line segments 
, 
, and 
are drawn with 
on 
, 
on 
, and 
on 
(see the figure at right). Given that 
, 
, 
, 
, and 
, find the area of .
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
