Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 10B Problems/Problem 23"

m (fixed minor grammar error)
Line 7: Line 7:
  
 
== Solution ==
 
== Solution ==
−
To help in finding the area of the quadrilateral, draw an [[auxillary line]] from the top vertex to the intersection of the two lines.  
+
To help in finding the [[area]] of the [[quadrilateral]], draw an auxillary line from the top [[vertex]] to the intersection of the two lines.  
  
−
Doing so, and labling the points yeilds this as the resulting diagram:  
+
Doing so and labling the [[point]]s yeilds this as the resulting diagram:  
  
 
[[Image:2006amc10b23solution.gif]]
 
[[Image:2006amc10b23solution.gif]]
  
−
Since triangles <math>AFC</math> and <math>EFC</math> share an altitude, and their respective areas are equal, their bases must be equal.  
+
Since [[triangle]]s <math>AFC</math> and <math>EFC</math> share an [[altitude]] from <math>C</math> and have equal area, their bases must be equal.  
  
 
So <math>AF=EF</math>.  
 
So <math>AF=EF</math>.  
  
−
Since triangles <math>AFB</math> and <math>EFB</math> share an altitude, and their respective bases are equal, their areas must be equal.  
+
Since triangles <math>AFB</math> and <math>EFB</math> share an altitude from <math>B</math> and their respective bases are equal, their areas must be equal.  
  
 
So <math>x+3=y</math>.  
 
So <math>x+3=y</math>.  
  
−
Since triangles <math>DFA</math> and <math>CFA</math> share an altitude, and their  respective areas are in the ratio <math>3:7</math>, their bases must be in the same ratio.  
+
Since triangles <math>DFA</math> and <math>CFA</math> share an altitude from <math>A</math> and their  respective areas are in the ratio <math>3:7</math>, their bases must be in the same ratio.  
  
 
So <math>\frac{DF}{3}=\frac{CF}{7}</math>.
 
So <math>\frac{DF}{3}=\frac{CF}{7}</math>.
  
−
Since triangles <math>DFB</math> and <math>CFB</math> share an altitude, and their  respective bases are in the ratio <math>3:7</math>, their areas must be in the same ratio.  
+
Since triangles <math>DFB</math> and <math>CFB</math> share an altitude from <math>B</math> and their  respective bases are in the ratio <math>3:7</math>, their areas must be in the same ratio.  
  
 
So <math>\frac{x}{3}=\frac{y+7}{7}</math>.
 
So <math>\frac{x}{3}=\frac{y+7}{7}</math>.

Revision as of 13:45, 29 July 2006

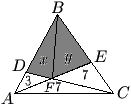
Problem

A triangle is partitioned into three triangles and a quadrilateral by drawing two lines from vertices to their opposite sides. The areas of the three triangles are 3, 7, and 7 as shown. What is the area of the shaded quadrilateral?

2006amc10b23.gif

$\mathrm{(A) \ } 15\qquad \mathrm{(B) \ } 17\qquad \mathrm{(C) \ } \frac{35}{2}\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } \frac{55}{3}$

Solution

To help in finding the area of the quadrilateral, draw an auxillary line from the top vertex to the intersection of the two lines.

Doing so and labling the points yeilds this as the resulting diagram:

2006amc10b23solution.gif

Since triangles $AFC$ and $EFC$ share an altitude from $C$ and have equal area, their bases must be equal.

So $AF=EF$.

Since triangles $AFB$ and $EFB$ share an altitude from $B$ and their respective bases are equal, their areas must be equal.

So $x+3=y$.

Since triangles $DFA$ and $CFA$ share an altitude from $A$ and their respective areas are in the ratio $3:7$, their bases must be in the same ratio.

So $\frac{DF}{3}=\frac{CF}{7}$.

Since triangles $DFB$ and $CFB$ share an altitude from $B$ and their respective bases are in the ratio $3:7$, their areas must be in the same ratio.

So $\frac{x}{3}=\frac{y+7}{7}$.

Substituting $x+3$ for $y$:

$\frac{x}{3}=\frac{x+3+7}{7}$

$\frac{x}{3}=\frac{x+10}{7}$

$7x=3x+30$

$4x=30$

$x=\frac{15}{2}$

$y=\frac{21}{2}$

Therefore, the shaded area is $x+y = \frac{15}{2} + \frac{21}{2} = 18 \Rightarrow D$

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_23&oldid=8743"