Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 10B Problems/Problem 15"

(Added problem and solution)
m (→‎Solution)
Line 13: Line 13:
 
<math> \angle ADC = \angle ABC = 120 ^\circ </math>.
 
<math> \angle ADC = \angle ABC = 120 ^\circ </math>.
  
−
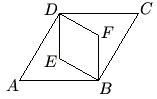
It is easy to see that rhombus <math>ABCD</math> is made up of equilateral triangles <math>DAB</math> and <math>DCB</math>.
+
It is easy to see that rhombus <math>ABCD</math> is made up of [[equilateral triangle]]s <math>DAB</math> and <math>DCB</math>.
  
 
Let the lengths of the sides of rhombus <math>ABCD</math> be <math>s</math>.  
 
Let the lengths of the sides of rhombus <math>ABCD</math> be <math>s</math>.  
  
−
The longer diagonal of rhombus <math>BFDE</math> is <math>BD</math>. Since <math>BD</math> is a side of an equilateral triangle with a side length of <math>s</math>, <math> BD = s </math>.
+
The longer [[diagonal]] of rhombus <math>BFDE</math> is <math>BD</math>. Since <math>BD</math> is a side of an equilateral triangle with a side length of <math>s</math>, <math> BD = s </math>.
  
 
The longer diagonal of rhombus <math>ABCD</math> is <math>AC</math>. Since <math>AC</math> is twice the length of an altitude of of an equilateral triangle with a side length of <math>s</math>, <math> AC = 2 \cdot \frac{s\sqrt{3}}{2} = s\sqrt{3} </math>
 
The longer diagonal of rhombus <math>ABCD</math> is <math>AC</math>. Since <math>AC</math> is twice the length of an altitude of of an equilateral triangle with a side length of <math>s</math>, <math> AC = 2 \cdot \frac{s\sqrt{3}}{2} = s\sqrt{3} </math>
Line 23: Line 23:
 
The ratio of the longer diagonal of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \frac{s}{s\sqrt{3}} = \frac{\sqrt{3}}{3} </math>
 
The ratio of the longer diagonal of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \frac{s}{s\sqrt{3}} = \frac{\sqrt{3}}{3} </math>
  
−
Therefore, the ratio of the area of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \left( \frac{\sqrt{3}}{3} \right) ^2 = \frac{1}{3} </math>
+
Therefore, the ratio of the [[area]] of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \left( \frac{\sqrt{3}}{3} \right) ^2 = \frac{1}{3} </math>
  
 
Let <math>x</math> be the area of rhombus <math>BFDE</math>.  
 
Let <math>x</math> be the area of rhombus <math>BFDE</math>.  

Revision as of 10:31, 29 July 2006

Problem

Rhombus $ABCD$ is similar to rhombus $BFDE$. The area of rhombus $ABCD$ is $24$ and $\angle BAD = 60^\circ$. What is the area of rhombus $BFDE$?

2006amc10b15.gif

$\mathrm{(A) \ } 6\qquad \mathrm{(B) \ } 4\sqrt{3}\qquad \mathrm{(C) \ } 8\qquad \mathrm{(D) \ } 9\qquad \mathrm{(E) \ } 6\sqrt{3}$

Solution

Using properties of a rhombus:

$\angle DAB = \angle DCB = 60 ^\circ$.

$\angle ADC = \angle ABC = 120 ^\circ$.

It is easy to see that rhombus $ABCD$ is made up of equilateral triangles $DAB$ and $DCB$.

Let the lengths of the sides of rhombus $ABCD$ be $s$.

The longer diagonal of rhombus $BFDE$ is $BD$. Since $BD$ is a side of an equilateral triangle with a side length of $s$, $BD = s$.

The longer diagonal of rhombus $ABCD$ is $AC$. Since $AC$ is twice the length of an altitude of of an equilateral triangle with a side length of $s$, $AC = 2 \cdot \frac{s\sqrt{3}}{2} = s\sqrt{3}$

The ratio of the longer diagonal of rhombus $BFDE$ to rhombus $ABCD$ is $\frac{s}{s\sqrt{3}} = \frac{\sqrt{3}}{3}$

Therefore, the ratio of the area of rhombus $BFDE$ to rhombus $ABCD$ is $\left( \frac{\sqrt{3}}{3} \right) ^2 = \frac{1}{3}$

Let $x$ be the area of rhombus $BFDE$.

$\frac{x}{24} = \frac{1}{3}$

$x = 8 \Rightarrow C$

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_15&oldid=8736"