Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 2 2006-2007 Problems"

m (→‎Problem 1)
m (→‎Problem 1)
Line 1: Line 1:
 
== Problem 1 ==
 
== Problem 1 ==
−
A positive integer is called a dragon if it can be partitioned into four positive integers <math>\displaystyle a,b,c,</math> and <math>\displaystyle d</math> such that <math>\displaystyle a+4=b-4=4c=d/4.</math> Find the smallest dragon.
+
A positive integer is called a ''dragon'' if it can be written as the sum of four positive integers <math>\displaystyle a,b,c,</math> and <math>\displaystyle d</math> such that <math>\displaystyle a+4=b-4=4c=d/4.</math> Find the smallest dragon.
  
 
[[Mock_AIME_2_2006-2007/Problem_1|Solution]]
 
[[Mock_AIME_2_2006-2007/Problem_1|Solution]]

Revision as of 11:25, 15 September 2006

Problem 1

A positive integer is called a dragon if it can be written as the sum of four positive integers $\displaystyle a,b,c,$ and $\displaystyle d$ such that $\displaystyle a+4=b-4=4c=d/4.$ Find the smallest dragon.

Solution

Problem 2

The set $\displaystyle S$ consists of all integers from $\displaystyle 1$ to $\displaystyle 2007,$ inclusive. For how many elements $\displaystyle n$ in $\displaystyle S$ is $\displaystyle f(n) = \frac{2n^3+n^2-n-2}{n^2-1}$ an integer?

Solution

Problem 3

Let $\displaystyle S$ be the sum of all positive integers $\displaystyle n$ such that $\displaystyle n^2+12n-2007$ is a perfect square. Find the remainder when $\displaystyle S$ is divided by $\displaystyle 1000.$

Solution

Problem 4

Let $\displaystyle n$ be the smallest positive integer for which there exist positive real numbers $\displaystyle a$ and $\displaystyle b$ such that $\displaystyle (a+bi)^n=(a-bi)^n$. Compute $\displaystyle \frac{b^2}{a^2}$.

Solution

Problem 5

Given that $\displaystyle iz^2=1+\frac 2z + \frac{3}{z^2}+\frac{4}{z ^3}+\frac{5}{z^4}+\cdots$ and $\displaystyle z=n\pm \sqrt{-i},$ find $\displaystyle \lfloor 100n \rfloor.$

Solution

Problem 6

If $\displaystyle \tan 15^\circ \tan 25^\circ \tan 35^\circ =\tan \theta$ and $\displaystyle 0^\circ \le \theta \le 180^\circ,$ find $\displaystyle \theta.$

Solution

Problem 7

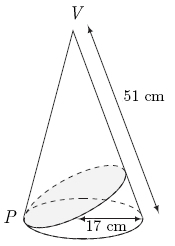
A right circular cone of base radius $\displaystyle 17$cm and slant height $\displaystyle 34$cm is given. $\displaystyle P$ is a point on the circumference of the base and the shortest path from $\displaystyle P$ around the cone and back is drawn (see diagram). If the length of this path is $\displaystyle m\sqrt{n},$ where $\displaystyle m$ and $\displaystyle n$ are relatively prime positive integers, find $\displaystyle m+n.$

Mock AIME 2 2007 Problem8.jpg

Solution

Problem 8

The positive integers $\displaystyle x_1, x_2, ... , x_7$ satisfy $\displaystyle x_6 = 144$ and $\displaystyle x_{n+3} = x_{n+2}(x_{n+1}+x_n)$ for $\displaystyle n = 1, 2, 3, 4$. Find the last three digits of $\displaystyle x_7$.

Solution

Problem 9

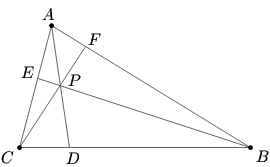
In right triangle $\displaystyle ABC,$ $\displaystyle \angle C=90^\circ.$ Cevians $\displaystyle AX$ and $\displaystyle BY$ intersect at $\displaystyle P$ and are drawn to $\displaystyle BC$ and $\displaystyle AC$ respectively such that $\displaystyle \frac{BX}{CX}=\frac23$ and $\displaystyle \frac{AY}{CY}=\sqrt 3.$ If $\displaystyle \tan \angle APB= \frac{a+b\sqrt{c}}{d},$ where $\displaystyle a,b,$ and $\displaystyle d$ are relatively prime and $\displaystyle c$ has no perfect square divisors excluding $\displaystyle 1,$ find $\displaystyle a+b+c+d.$

Solution

Problem 10

Find the number of solutions, in degrees, to the equation $\displaystyle \sin^{10}x + \cos^{10}x = \frac{29}{16}\cos^4 2x,$ where $\displaystyle 0^\circ \le x^\circ \le 2007^\circ.$

Solution

Problem 11

Find the sum of the squares of the roots, real or complex, of the system of simultaneous equations

$\displaystyle x+y+z=3,~x^2+y^2+z^2=3,~x^3+y^3+z^3 =3.$

Solution

Problem 12

In quadrilateral $\displaystyle ABCD,$ $\displaystyle m \angle DAC= m\angle DBC$ and $\displaystyle \frac{[ADB]}{[ABC]}=\frac12.$ If $\displaystyle AD=4,$ $\displaystyle BC=6$, $\displaystyle BO=1,$ and the area of $\displaystyle ABCD$ is $\displaystyle \frac{a\sqrt{b}}{c},$ where $\displaystyle a,b,c$ are relatively prime positive integers, find $\displaystyle a+b+c.$


Note*: $\displaystyle[ABC]$ and $\displaystyle[ADB]$ refer to the areas of triangles $\displaystyle ABC$ and $\displaystyle ADB.$

Solution

Problem 13

In his spare time, Richard Rusczyk shuffles a standard deck of 52 playing cards. He then turns the cards up one by one from the top of the deck until the third ace appears. If the expected (average) number of cards Richard will turn up is $\displaystyle m/n,$ where $\displaystyle m$ and $\displaystyle n$ are relatively prime positive integers, find $\displaystyle m+n.$

Solution

Problem 14

In triangle ABC, $\displaystyle AB = 308$ and $\displaystyle AC=35.$ Given that $\displaystyle AD$, $\displaystyle BE,$ and $\displaystyle CF,$ intersect at $\displaystyle P$ and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of $\displaystyle BC.$

Mock AIME 2 2007 Problem14.jpg

Solution

Problem 15

A $\displaystyle 4\times4\times4$ cube is composed of $\displaystyle 64$ unit cubes. The faces of $\displaystyle 16$ unit cubes are colored red. An arrangement of the cubes is $\mathfrak{Intriguing}$ if there is exactly $\displaystyle 1$ red unit cube in every $\displaystyle 1\times1\times4$ rectangular box composed of $\displaystyle 4$ unit cubes. Determine the number of $\mathfrak{Intriguing}$ colorings.

Solution

CubeArt.jpg

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_2_2006-2007_Problems&oldid=10113"