Difference between revisions of "2021 AIME I Problems/Problem 11"
MRENTHUSIASM (talk | contribs) (→Solution 4 (Cyclic Quadrilaterals and Similar Triangles)) |
MRENTHUSIASM (talk | contribs) (→Solution 4 (Cyclic Quadrilaterals and Similar Triangles)) |
||
| Line 77: | Line 77: | ||
~MRENTHUSIASM (inspired by Math Jams's <b>2021 AIME I Discussion</b>) | ~MRENTHUSIASM (inspired by Math Jams's <b>2021 AIME I Discussion</b>) | ||
| − | ===Solution 4.2 (Area Formulas)=== | + | ===Solution 4.2 (Area Formulas and Ptolemy's Theorem)=== |
Let the brackets denote areas. By Brahmagupta's Formula, we get <cmath>[ABCD]=\sqrt{(s-AB)(s-BC)(s-CD)(s-DA)}=2\sqrt{210},</cmath> where <math>s=\frac{AB+BC+CD+DA}{2}</math> is the semiperimeter of <math>ABCD.</math> | Let the brackets denote areas. By Brahmagupta's Formula, we get <cmath>[ABCD]=\sqrt{(s-AB)(s-BC)(s-CD)(s-DA)}=2\sqrt{210},</cmath> where <math>s=\frac{AB+BC+CD+DA}{2}</math> is the semiperimeter of <math>ABCD.</math> | ||
| − | By area addition, we get | + | Note that <math>\sin(180^\circ-\theta)=\sin\theta</math> holds for all <math>\theta.</math> By area addition and Ptolemy's Theorem, we get |
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
[ABCD]&=[ABE]+[BCE]+[CDE]+[DAE] \\ | [ABCD]&=[ABE]+[BCE]+[CDE]+[DAE] \\ | ||
&=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin(180^\circ-\theta)+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin(180^\circ-\theta) \\ | &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin(180^\circ-\theta)+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin(180^\circ-\theta) \\ | ||
&=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin\theta+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin\theta \\ | &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin\theta+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin\theta \\ | ||
| − | &=\frac12\cdot\sin\theta\cdot(AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE) | + | &=\frac12\cdot\sin\theta\cdot(AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE) \\ |
| + | &=\frac12\cdot\sin\theta\cdot\left((AE+CE)\cdot(BE+DE)\right) \\ | ||
| + | &=\frac12\cdot\sin\theta\cdot\left(AC\cdot BD\right) \\ | ||
| + | &=\frac12\cdot\sin\theta\cdot\left(AB\cdot CD+BC\cdot DA\right) \\ | ||
| + | &=\frac{59}{2}\cdot\sin\theta. | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | Finally, substituting this result into <math>(\bigstar)</math> gives <math>22\cos\theta=\frac{242}{59},</math> from which the answer is <math>242+59=\boxed{301}.</math> | ||
| − | + | ~MRENTHUSIASM | |
| + | |||
| + | ===Remark=== | ||
| + | In <math>ABCD,</math> we have | ||
| + | <cmath>\begin{align*} | ||
| + | AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE &= (AE+CE)\cdot(BE+DE) \\ | ||
| + | &= AC\cdot BD \\ | ||
| + | &= AB\cdot CD+BC\cdot DA | ||
| + | \end{align*}</cmath> | ||
| + | ~MRENTHUSIASM | ||
==See also== | ==See also== | ||
{{AIME box|year=2021|n=I|num-b=10|num-a=12}} | {{AIME box|year=2021|n=I|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 21:33, 29 May 2021
Contents
Problem
Let ![]() be a cyclic quadrilateral with
be a cyclic quadrilateral with ![]() and
and ![]() . Let
. Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() , respectively, to line
, respectively, to line ![]() and let
and let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() . The perimeter of
. The perimeter of ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
~MRENTHUSIASM (by Geometry Expressions)
Solution 1
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Let
. Let ![]() .
.
Firstly, since ![]() , we deduce that
, we deduce that ![]() is cyclic. This implies that
is cyclic. This implies that ![]() , with a ratio of
, with a ratio of ![]() . This means that
. This means that ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence ![]() It therefore only remains to find
It therefore only remains to find ![]() .
.
From Ptolemy's theorem, we have that ![]() . From Brahmagupta's Formula,
. From Brahmagupta's Formula, ![]() . But the area is also
. But the area is also ![]() , so
, so ![]() . Then the desired fraction is
. Then the desired fraction is ![]() for an answer of
for an answer of ![]() .
.
Solution 2 (Finding cos x)
The angle ![]() between diagonals satisfies
between diagonals satisfies ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}\]](http://latex.artofproblemsolving.com/9/7/c/97c3d3b8825eea07df794427667b774cbf27b7c8.png) (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus,
(see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus, ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}\]](http://latex.artofproblemsolving.com/8/9/9/899281a447db8934bc4dce2667cc8ad64656fb4d.png) or
or ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}\]](http://latex.artofproblemsolving.com/f/8/b/f8b3a3a8c72ce4ff55ed062a76e4ebc8147f633b.png) That is,
That is, ![]() or
or ![]() Thus,
Thus, ![]() or
or ![]()
![]() In this context,
In this context, ![]() . Thus,
. Thus, ![]()
![]()
![]() ~y.grace.yu
~y.grace.yu
Solution 3 (Pythagorean Theorem)
We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length ![]() [I don't believe this is correct... are the two diagonals of
[I don't believe this is correct... are the two diagonals of ![]() necessarily congruent? -peace09] WLOG we focus on diagonal
necessarily congruent? -peace09] WLOG we focus on diagonal ![]() To find the diagonal of the inner quadrilateral, we drop the altitude from
To find the diagonal of the inner quadrilateral, we drop the altitude from ![]() and
and ![]() and calculate the length of
and calculate the length of ![]() Let
Let ![]() be
be ![]() (Thus
(Thus ![]() By Pythagorean theorem, we have
By Pythagorean theorem, we have ![]() Now let
Now let ![]() be
be ![]() (thus making
(thus making ![]() ). Similarly, we have
). Similarly, we have ![]() We see that
We see that ![]() , the scaled down diagonal is just
, the scaled down diagonal is just ![]() which is
which is ![]() times our original diagonal
times our original diagonal ![]() implying a scale factor of
implying a scale factor of ![]() Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply
Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply ![]() making our answer
making our answer ![]() -fidgetboss_4000
-fidgetboss_4000
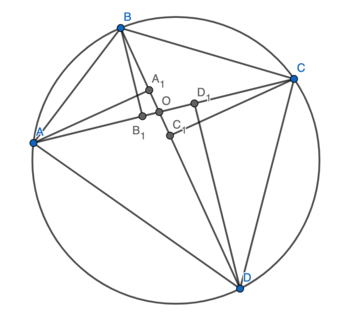
Solution 4 (Cyclic Quadrilaterals and Similar Triangles)
This solution refers to the Diagram section.
Suppose ![]() and
and ![]() intersect at
intersect at ![]() and let
and let ![]()
By the Converse of the Inscribed Angle Theorem, if distinct points ![]() and
and ![]() lie on the same side of
lie on the same side of ![]() (but not on
(but not on ![]() itself) for which
itself) for which ![]() then
then ![]() and
and ![]() are cyclic. From the Converse of the Inscribed Angle Theorem, quadrilaterals
are cyclic. From the Converse of the Inscribed Angle Theorem, quadrilaterals ![]() and
and ![]() are all cyclic.
are all cyclic.
We obtain the following diagram:
In every cyclic quadrilateral, each pair of opposite angles is supplementary. So, we have ![]() and
and ![]() by angle chasing, from which
by angle chasing, from which ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![\[\frac{A_1B_1}{AB}=\underbrace{\frac{A_1E}{AE}}_{\substack{\text{right} \\ \triangle A_1AE}}=\underbrace{\frac{B_1E}{BE}}_{\substack{\text{right} \\ \triangle B_1BE}}=\cos\theta. \hspace{15mm}(1)\]](http://latex.artofproblemsolving.com/d/4/d/d4db43e8608477497fbb257d17bfe041000b4d5f.png) Similarly, we have
Similarly, we have ![]() and
and ![]() by angle chasing, from which
by angle chasing, from which ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![\[\frac{C_1D_1}{CD}=\underbrace{\frac{C_1E}{CE}}_{\substack{\text{right} \\ \triangle C_1CE}}=\underbrace{\frac{D_1E}{DE}}_{\substack{\text{right} \\ \triangle D_1DE}}=\cos\theta. \hspace{14.75mm}(2)\]](http://latex.artofproblemsolving.com/6/2/f/62f9cf8e1812c9bd4aaec0b5a8408cea5a37f597.png) We apply the Transitive Property to
We apply the Transitive Property to ![]() and
and ![]()
- We get
 from which
from which  by SAS, with the ratio of similitude
by SAS, with the ratio of similitude ![\[\frac{B_1C_1}{BC}=\frac{B_1E}{BE}=\frac{C_1E}{CE}=\cos\theta. \hspace{14.75mm}(3)\]](//latex.artofproblemsolving.com/3/2/1/32130f85d69205e70793791c48e5faefed46e1fd.png)
- We get
 from which
from which  by SAS, with the ratio of similitude
by SAS, with the ratio of similitude ![\[\frac{D_1A_1}{DA}=\frac{D_1E}{DE}=\frac{A_1E}{AE}=\cos\theta. \hspace{14mm}(4)\]](//latex.artofproblemsolving.com/1/1/5/115bc444769d7d350cdfbdf6c13c34ddfd82fa06.png)
From ![]() and
and ![]() The perimeter of
The perimeter of ![]() is
is
 Two solutions follow from here:
Two solutions follow from here:
Solution 4.1 (Law of Cosines and Ptolemy's Theorem)
Note that ![]() holds for all
holds for all ![]() We apply the Law of Cosines to
We apply the Law of Cosines to ![]() and
and ![]() respectively:
respectively:
 We subtract
We subtract ![]() from
from ![]() factor the result, and apply Ptolemy's Theorem to
factor the result, and apply Ptolemy's Theorem to ![]()
![\begin{align*} 2\cdot\cos\theta\cdot(AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE)&=22 &&\hspace{5mm}[(2\star)+(4\star)]-[(1\star)+(3\star)] \\ \cos\theta\cdot(AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE)&=11 \\ \cos\theta\cdot\left((AE+CE)\cdot(BE+DE)\right)&=11 &&\hspace{5mm}\text{Factor} \\ \cos\theta\cdot\left(AC\cdot BD\right)&=11 \\ \cos\theta\cdot\left(AB\cdot CD+BC\cdot DA\right)&=11 &&\hspace{5mm}\text{Ptolemy's Theorem on }ABCD \\ \cos\theta\cdot59&=11 \\ \cos\theta&=\frac{11}{59}. \end{align*}](http://latex.artofproblemsolving.com/6/c/2/6c273c689c5ccbd2a65c7ac75cd201bf35045fb8.png) Finally, substituting this result into
Finally, substituting this result into ![]() gives
gives ![]() from which the answer is
from which the answer is ![]()
~MRENTHUSIASM (inspired by Math Jams's 2021 AIME I Discussion)
Solution 4.2 (Area Formulas and Ptolemy's Theorem)
Let the brackets denote areas. By Brahmagupta's Formula, we get ![]() where
where ![]() is the semiperimeter of
is the semiperimeter of ![]()
Note that ![]() holds for all
holds for all ![]() By area addition and Ptolemy's Theorem, we get
By area addition and Ptolemy's Theorem, we get
![\begin{align*} [ABCD]&=[ABE]+[BCE]+[CDE]+[DAE] \\ &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin(180^\circ-\theta)+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin(180^\circ-\theta) \\ &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin\theta+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin\theta \\ &=\frac12\cdot\sin\theta\cdot(AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE) \\ &=\frac12\cdot\sin\theta\cdot\left((AE+CE)\cdot(BE+DE)\right) \\ &=\frac12\cdot\sin\theta\cdot\left(AC\cdot BD\right) \\ &=\frac12\cdot\sin\theta\cdot\left(AB\cdot CD+BC\cdot DA\right) \\ &=\frac{59}{2}\cdot\sin\theta. \end{align*}](http://latex.artofproblemsolving.com/c/e/5/ce59b8570a03070b9f0ac8a3d8fae0e451710765.png) Finally, substituting this result into
Finally, substituting this result into ![]() gives
gives ![]() from which the answer is
from which the answer is ![]()
~MRENTHUSIASM
Remark
In ![]() we have
we have
 ~MRENTHUSIASM
~MRENTHUSIASM
See also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.