Difference between revisions of "2021 JMPSC Sprint Problems/Problem 13"
Lamboreghini (talk | contribs) (→Solution) |
Lamboreghini (talk | contribs) (→Solution) |
||
| Line 7: | Line 7: | ||
==Solution== | ==Solution== | ||
By the [[Pythagorean Theorem]], we have that the diameter of the cylinder's base is 15 units long. Thus, the cylinder's base has radius <math>\frac{15}{2}</math> units. Thus, the volume of the cylinder is <math>\left(\frac{15}{2}\right)^2\cdot8\pi=\boxed{450}\pi.</math> | By the [[Pythagorean Theorem]], we have that the diameter of the cylinder's base is 15 units long. Thus, the cylinder's base has radius <math>\frac{15}{2}</math> units. Thus, the volume of the cylinder is <math>\left(\frac{15}{2}\right)^2\cdot8\pi=\boxed{450}\pi.</math> | ||
| + | |||
| + | ~Lamboreghini | ||
Revision as of 23:21, 10 July 2021
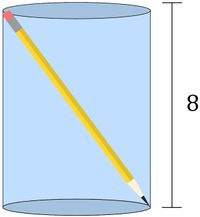
Problem
Grace places a pencil in a cylindrical cup and is surprised to see that it fits diagonally. The pencil is 
units long and of negligible thickness. The cup is 
units tall. The volume of the cup can be written as 
cubic units. Find 
.
Solution
By the Pythagorean Theorem, we have that the diameter of the cylinder's base is 15 units long. Thus, the cylinder's base has radius 
units. Thus, the volume of the cylinder is 
~Lamboreghini
