Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 IMO Problems/Problem 6"

(→‎Solution)
(→‎Solution)
Line 4: Line 4:
  
 
==Solution==
 
==Solution==
−
[[File:2019 6 s1.png|500px|right]]
+
[[File:2019 6 s1.png|450px|right]]
 +
[[File:2019 6 s2.png|450px|right]]
 
<i><b>Step 1</b></i>
 
<i><b>Step 1</b></i>
  
Line 25: Line 26:
  
 
<i><b>Step 2</b></i>
 
<i><b>Step 2</b></i>
 +
 +
We find a simplified way to define the point <math>Q.</math>
 +
 +
We define <math>\angle BAC = 2 \alpha \implies \angle AFE = \angle AEF = 90^\circ – \alpha \implies</math>
 +
<math>\angle BFE = \angle CEF = 180^\circ – (90^\circ – \alpha) = 90^\circ + \alpha =  \angle BIC</math>
 +
<math>(AI, BI,</math> and <math>CI</math> are bisectrices).
 +
We use the Tangent-Chord Theorem and get <math>\angle EPF = \angle AEF = 90^\circ – \alpha.</math>
 +
 +
<math>\angle BQC =  \angle BQP +  \angle PQC = \angle BFP + \angle CEP =</math>
 +
<math>=\angle BFE – \angle EFP + \angle CEF – \angle FEP =</math>
 +
<math>= 90^\circ + \alpha + 90^\circ + \alpha – (90^\circ + \alpha) = </math>
 +
<math>90^\circ + \alpha = \angle BIC \implies</math>
 +
 +
points <math>Q, B, I,</math> and <math>C</math> are concyclic.

Revision as of 12:03, 29 August 2022

Problem

Let $I$ be the incenter of acute triangle $ABC$ with $AB \neq AC$. The incircle $\omega$ of $ABC$ is tangent to sides $BC$, $CA$, and $AB$ at $D$, $E$, and $F$, respectively. The line through $D$ perpendicular to $EF$ meets $\omega$ again at $R$. Line $AR$ meets ω again at $P$. The circumcircles of triangles $PCE$ and $PBF$ meet again at $Q$. Prove that lines $DI$ and $PQ$ meet on the line through $A$ perpendicular to $AI$.

Solution

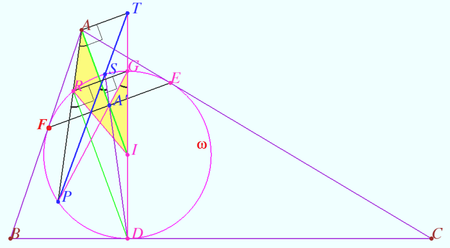
2019 6 s1.png
2019 6 s2.png

Step 1

We find an auxiliary point $S.$

Let $G$ be the antipode of $D$ on $\omega, GD = 2R,$ where $R$ is radius $\omega.$

We define $A' = PG \cap AI.$

$RD||AI, PRGD$ is cyclic $\implies \angle IAP = \angle DRP = \angle DGP.$

$RD||AI, RD \perp RG, RI=GI \implies \angle AIR = \angle AIG \implies$ \[\triangle AIR \sim \triangle GIA' \implies \frac {AI}{GI} = \frac {RI}{A'I}\implies A'I \cdot AI = R^2.\] An inversion with respect $\omega$ swap $A$ and $A' \implies A'$ is the midpoint $EF.$

Let $DA'$ meets $\omega$ again at $S.$ We define $T = PS \cap DI.$

Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega \implies DI$ and $PS$ meet on the line through $A$ perpendicular to $AI.$ The problem is reduced to proving that $Q \in PST.$

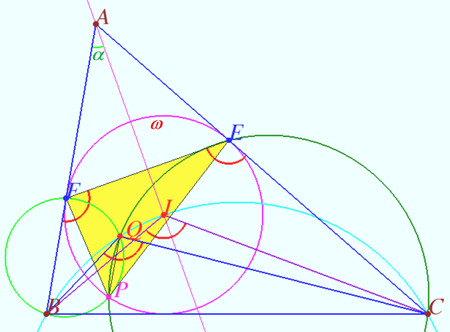
Step 2

We find a simplified way to define the point $Q.$

We define $\angle BAC = 2 \alpha \implies \angle AFE = \angle AEF = 90^\circ – \alpha \implies$ $\angle BFE = \angle CEF = 180^\circ – (90^\circ – \alpha) = 90^\circ + \alpha = \angle BIC$ $(AI, BI,$ and $CI$ are bisectrices). We use the Tangent-Chord Theorem and get $\angle EPF = \angle AEF = 90^\circ – \alpha.$

$\angle BQC = \angle BQP + \angle PQC = \angle BFP + \angle CEP =$ $=\angle BFE – \angle EFP + \angle CEF – \angle FEP =$ $= 90^\circ + \alpha + 90^\circ + \alpha – (90^\circ + \alpha) =$ $90^\circ + \alpha = \angle BIC \implies$

points $Q, B, I,$ and $C$ are concyclic.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_IMO_Problems/Problem_6&oldid=177660"