Difference between revisions of "Hook Length Theorem"
(→Theorem) |
|||
| Line 16: | Line 16: | ||
[[File:Hook Example.png|200px|center]] | [[File:Hook Example.png|200px|center]] | ||
| − | Let the product of all the hooks in a tableau be h.Then, the Hook Length Theorem states that the number of SYTs is < | + | Let the product of all the hooks in a tableau be h. Then, the Hook Length Theorem states that the number of SYTs is <math>\frac{n!}{h}</math>. |
Revision as of 20:48, 5 November 2022
Introduction
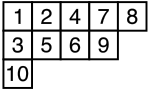
The hook length theorem is a theorem to be used on Standard Young Tableau. A standard Young Tableau is essentially a pack of blocks together, such as this one:
A tableau has a decreasing(not strictly decreasing) number of blocks in every row.
A Standard Young Tableau(SYT) has increasing numbers in both rows and columns. As shown in the figure, 1-3-10 is increasing, as well as 2-5, 4-6, 7-9, 1-2-4-7-8, and 3-5-6-9.
Theorem
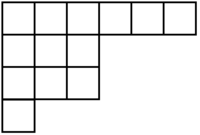
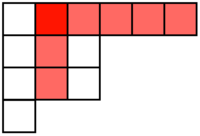
Let the number of blocks in the tableau be n. A hook of a block is the number of blocks to the right and below the block, including the block. In the below image, the hook of the red square is 7.
Let the product of all the hooks in a tableau be h. Then, the Hook Length Theorem states that the number of SYTs is ![]() .
.