Difference between revisions of "Hook Length Theorem"
(→Theorem) |
(→Theorem) |
||
| Line 16: | Line 16: | ||
[[File:Hook Example.png|200px|center]] | [[File:Hook Example.png|200px|center]] | ||
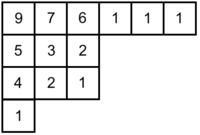
| − | Let the product of all the hooks in a tableau be <math>h</math>. Then, the Hook Length Theorem states that the number of SYTs is <math>\frac{n!}{h}</math>. | + | Let the product of all the hooks in a tableau be <math>h</math>. Then, the Hook Length Theorem states that the number of SYTs is <math>\frac{n!}{h}</math>. The number of hooks of each block in the example tableau is shown below. |
| + | |||
| + | [[File:TableauHook.png|200px|center]] | ||
| + | |||
| + | So in the example, the number of SYTs is <math>\frac{13!}{9\times7\times6\times1\times1\times1\times5\times3\times2\times4\times2\times1\times1} = 68640</math> | ||
Revision as of 20:56, 5 November 2022
Introduction
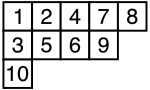
The hook length theorem is a theorem to be used on Standard Young Tableau. A standard Young Tableau is essentially a pack of blocks together, such as this one:
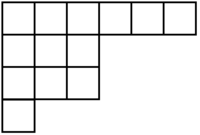
A tableau has a decreasing(not strictly decreasing) number of blocks in every row.
A Standard Young Tableau(SYT) has increasing numbers in both rows and columns. As shown in the figure, 1-3-10 is increasing, as well as 2-5, 4-6, 7-9, 1-2-4-7-8, and 3-5-6-9.
Theorem
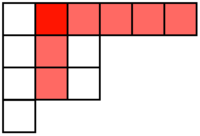
Let the number of blocks in the tableau be n. A hook of a block is the number of blocks to the right and below the block, including the block. In the below image, the hook of the red square is 
.
Let the product of all the hooks in a tableau be 
. Then, the Hook Length Theorem states that the number of SYTs is 
. The number of hooks of each block in the example tableau is shown below.
So in the example, the number of SYTs is 
