Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Miquel's point"

(→‎Miquel and Steiner's quadrilateral theorem)
(→‎Miquel and Steiner's quadrilateral theorem)
Line 1: Line 1:
 
==Miquel and Steiner's quadrilateral theorem==
 
==Miquel and Steiner's quadrilateral theorem==
−
[[Miquel circles|500px|right]]
+
[[File:4 Miquel circles.png|500px|right]]
 
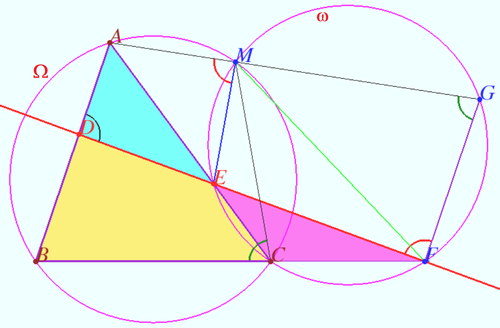
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
 
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
  
Line 7: Line 7:
 
<i><b>Proof</b></i>
 
<i><b>Proof</b></i>
  
−
Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF \omega</math> at point <math>M.</math>
+
Let circumcircle of <math>\triangle ABC</math> circle <math>\Omega</math> cross the circumcircle of <math>\triangle CEF</math> circle <math>\omega</math> at point <math>M.</math>
  
 
Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math>
 
Let <math>AM</math> cross <math>\omega</math> second time in the point <math>G.</math>
Line 13: Line 13:
 
<math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math>
 
<math>CMGF</math> is cyclic <math>\implies \angle BCM = \angle MGF.</math>
  
−
<math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies \angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math>
+
<math>AMCB</math> is cyclic <math>\implies \angle BCM + \angle BAM = 180^\circ \implies</math>
 +
 
 +
<math>\angle BAG + \angle AGF = 180^\circ \implies AB||GF.</math>
  
 
<math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math>
 
<math>CMGF</math> is cyclic <math>\implies \angle AME = \angle EFG.</math>
  
−
<math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math>
+
<math>AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies</math>
 +
 
 +
<math>ADEM</math> is cyclic and circumcircle of <math>\triangle ADE</math> contain the point <math>M.</math>
  
 
Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired.
 
Similarly circumcircle of <math>\triangle BDF</math> contain the point <math>M</math> as desired.

Revision as of 09:18, 5 December 2022

Miquel and Steiner's quadrilateral theorem

4 Miquel circles.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcircles of all four triangles meet at a single point.

Proof

Let circumcircle of $\triangle ABC$ circle $\Omega$ cross the circumcircle of $\triangle CEF$ circle $\omega$ at point $M.$

Let $AM$ cross $\omega$ second time in the point $G.$

$CMGF$ is cyclic $\implies \angle BCM = \angle MGF.$

$AMCB$ is cyclic $\implies \angle BCM + \angle BAM = 180^\circ \implies$

$\angle BAG + \angle AGF = 180^\circ \implies AB||GF.$

$CMGF$ is cyclic $\implies \angle AME = \angle EFG.$

$AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies$

$ADEM$ is cyclic and circumcircle of $\triangle ADE$ contain the point $M.$

Similarly circumcircle of $\triangle BDF$ contain the point $M$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Circle of circumcenters

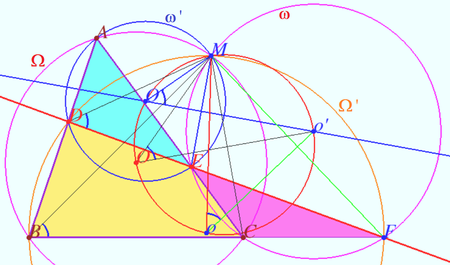
Miquel point.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcenters of all four triangles and point $M$ are concyclic.

Proof

Let $\Omega, \omega, \Omega',$ and $\omega'$ be the circumcircles of $\triangle ABC, \triangle CEF, \triangle BDF,$ and $\triangle ADE,$ respectively.

In $\Omega' \angle MDF = \angle MBF.$

In $\omega' \angle MDE = \frac {\overset{\Large\frown} {ME}} {2}.$

$ME$ is the common chord of $\omega$ and $\omega' \implies \angle MOE = \overset{\Large\frown} {ME} \implies$

\[\angle MO'o' = \frac {\overset{\Large\frown} {ME}} {2} = \angle MDE.\]

Similarly, $MF$ is the common chord of $\omega$ and $\Omega' \implies \angle MDF = \angle Moo' = \angle MO'o'.$

Similarly, $MC$ is the common chord of $\Omega$ and $\omega' \implies \angle MBC = \angle MOo' \implies$

$\angle MOo' = \angle MO'o' \implies$ points $M, O, O', o,$ and $o'$ are concyclic as desired.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Miquel%27s_point&oldid=183607"