Difference between revisions of "Steiner line"

Revision as of 14:41, 7 December 2022

Steiner line

Let $ABC$ be a triangle with orthocenter $H. P$ is a point on the circumcircle $\Omega$ of $\triangle ABC.$

Let $P_A, P_B,$ and $P_C$ be the reflections of $P$ in three lines which contains edges $BC, AC,$ and $AB,$ respectively.

Prove that $P_A, P_B, P_C,$ and $H$ are collinear. Respective line is known as the Steiner line of point $P$ with respect to $\triangle ABC.$

Proof

Let $D, E,$ and $F$ be the foots of the perpendiculars dropped from $P$ to lines $AB, AC,$ and $BC,$ respectively.

WLOG, Steiner line cross $AB$ at $Y$ and $AC$ at $Z.$

The line $DEF$ is Simson line of point $P$ with respect of $\triangle ABC.$

$D$ is midpoint of segment $PP_C \implies$ homothety centered at $P$ with ratio $2$ sends point $D$ to a point $P_C.$

Similarly, this homothety sends point $E$ to a point $P_B$ , point $F$ to a point $P_A,$ therefore this homothety send Simson line to line $P_AP_BP_C.$

Let $\angle ABC = \beta, \angle BFD = \varphi \implies \angle BDF = \beta – \varphi.$ $P_CP_A||DF \implies \angle P_CYB = \beta – \varphi.$ $P$ is simmetric to $P_C \implies \angle PYD = \beta – \varphi.$

Quadrungle $BDPF$ is cyclic $\implies \angle BPD = \varphi \implies \angle BPY = 90^\circ – \angle BYP – \angle BPD = 90^\circ – \beta.$

$\angle BCH = \angle BPY \implies PY \cap CH$ at point $H_C \in \Omega.$ Similarly, line $BH \cap PZ$ at $H_B \in \Omega.$

According the Collins Claim $YZ$ is $H-line,$ therefore $H \in P_AP_B.$

Simson line

vladimir.shelomovskii@gmail.com, vvsss

Collings Clime

Let triangle $ABC$ be the triangle with the orthocenter $H$ and circumcircle $\Omega.$ Denote $H–line$ any line containing point $H.$

Let $l_A, l_B,$ and $l_C$ be the reflections of $H-line$ in the edges $BC, AC,$ and $AB,$ respectively.

Prove that lines $l_A, l_B,$ and $l_C$ are concurrent and the point of concurrence lies on $\Omega.$

Proof

Let $D, E,$ and $F$ be the crosspoints of $H–line$ with $AB, AC,$ and $BC,$ respectively.

WLOG $D \in AB, E \in AC.$ Let $H_A, H_B,$ and $H_C$ be the points symmetric to $H$ with respect $BC, AC,$ and $AB,$ respectively.

Therefore $H_A \in l_A, H_B \in l_B, H_C \in l_C,$ $AH = AH_B = AH_C, BH = BH_A = BH_C, CH = CH_A = CH_B \implies$ $\angle HH_BE = \angle EHH_B = \angle BHD = \angle BH_CD.$

Let $P$ be the crosspoint of $l_B$ and $l_C \implies BH_CH_BP$ is cyclic $\implies P \in \Omega.$

Similarly $\angle CH_BE = \angle CHE = \angle CH_A \implies CH_BH_AP$ is cyclic $\implies P \in \Omega \implies$ the crosspoint of $l_B$ and $l_A$ is point $P.$

Usually the point $P$ is called the anti-Steiner point of the $H-line$ with respect to $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Ortholine

Let four lines made four triangles of a complete quadrilateral.

In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $H, H_A, H_B,$ and $H_C$ be the orthocenters of $\triangle ABC, \triangle ADE, \triangle BDF,$ and $\triangle CEF,$ respectively.

Prove that points $H, H_A, H_B,$ and $H_C$ are collinear.

Proof

Let $M$ be Miquel point of a complete quadrilateral.

Line $KLMN$ is the line which contain $4$ Simson lines of $4$ triangles.

Using homothety centered at $M$ with ratio $2$ we get $4$ coinciding Stainer lines which contain points $H, H_A, H_B,$ and $H_C$ .

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 57: / Line 57: @@
 Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Ortholine==
+[[File:Ortholine.png|500px|right]]
+Let four lines made four triangles of a complete quadrilateral.
+In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
+Let points <math>H, H_A, H_B,</math> and <math>H_C</math> be the orthocenters of <math>\triangle ABC, \triangle ADE, \triangle BDF,</math> and <math>\triangle CEF,</math> respectively.
+Prove that points <math>H, H_A, H_B,</math> and <math>H_C</math> are collinear.
+<i><b>Proof</b></i>
+Let <math>M</math> be Miquel point of a complete quadrilateral.
+Line <math>KLMN</math> is the line which contain <math>4</math> Simson lines of <math>4</math> triangles.
+Using homothety centered at <math>M</math> with ratio <math>2</math> we get <math>4</math> coinciding Stainer lines which contain points <math>H, H_A, H_B,</math> and <math>H_C</math>.
+*[[Miquel’s point]]
+*[[Simson line]]
 '''vladimir.shelomovskii@gmail.com, vvsss'''

Page

Toolbox

Search

Difference between revisions of "Steiner line"

Revision as of 14:41, 7 December 2022

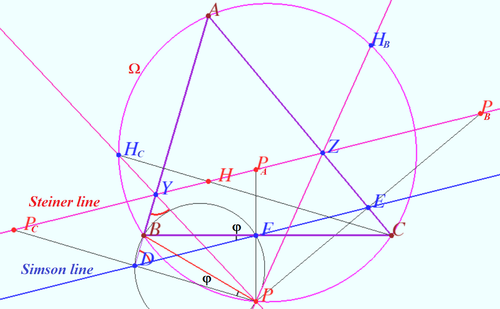
Steiner line

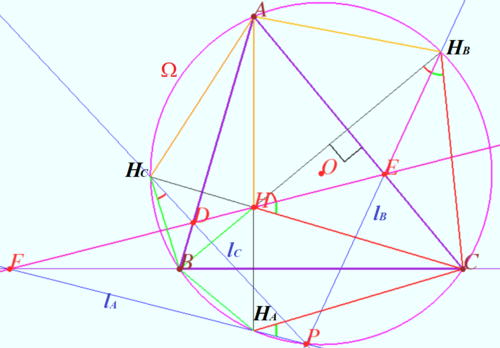
Collings Clime

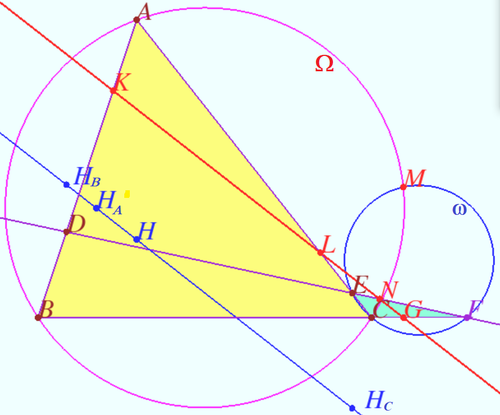
Ortholine