Difference between revisions of "Complete Quadrilateral"
(Created page with "==Complete quadrilateral== Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangl...") |
(→Complete quadrilateral) |
||
| Line 5: | Line 5: | ||
*[[Simson line]] | *[[Simson line]] | ||
*[[Steiner line]] | *[[Steiner line]] | ||
| + | |||
| + | ==Radical axis== | ||
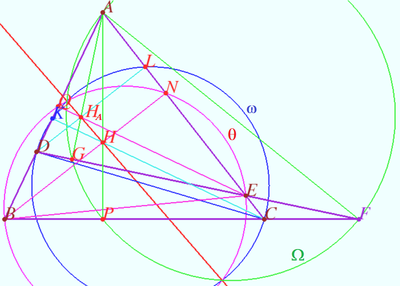
| + | [[File:Complete radical axes.png|400px|right]] | ||
| + | Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math> | ||
| + | |||
| + | Let points <math>H,</math> and <math>H_A</math> be the orthocenters of <math>\triangle ABC</math> and <math>\triangle ADE,</math> respectively. | ||
| + | |||
| + | Let circles <math>\omega, \theta,</math> and <math>\Omega</math> be the circles with diameters <math>CD, BE,</math> and <math>AF,</math> respectively. | ||
| + | Prove that Steiner line <math>HH_A</math> is the radical axis of <math>\omega, \theta,</math> and <math>\Omega.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let points <math>G, K, L, N, P,</math> and <math>Q</math> be the foots of perpendiculars <math>AH_A, CH, DH_A, BH, AH,</math> and <math>EH_A,</math> respectively. | ||
| + | |||
| + | Denote <math>Po(X)_{\omega}</math> power of point <math>X</math> with respect the circle <math>\omega.</math> | ||
| + | <cmath>\angle AGF = 90^\circ \implies G \in \Omega \implies Po(H_A)_{\Omega} = AH_A \cdot GH_A.</cmath> | ||
| + | <cmath>\angle CLD = 90^\circ \implies L \in \omega \implies Po(H_A)_{\omega} = DH_A \cdot LH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.</cmath> | ||
| + | <cmath>\angle EQB = 90^\circ \implies Q \in \theta \implies Po(H_A)_{\theta} = EH_A \cdot QH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.</cmath> | ||
| + | <cmath>\angle APF = 90^\circ \implies P \in \Omega \implies Po(H)_{\Omega} = AH \cdot PH_A.</cmath> | ||
| + | <cmath>\angle BNE = 90^\circ \implies N \in \theta \implies Po(H)_{\theta} = BH \cdot NH = AH \cdot PH = Po(H)_{\Omega}.</cmath> | ||
| + | <cmath>\angle CKD = 90^\circ \implies K \in \theta \implies Po(H)_{\omega} = CH \cdot KH = AH \cdot PH = Po(H)_{\Omega}.</cmath> | ||
| + | Therefore power of points <math>H</math> and <math>H_A</math> with respect these three circles are the same, these points lies on the common radical axis of <math>\omega, \theta,</math> and <math>\Omega \implies</math> Steiner line <math>HH_A</math> is the radical axis as desired. | ||
Revision as of 15:31, 9 December 2022
Complete quadrilateral
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]() One can see some of the properties of this configuration and their proof using the following links.
One can see some of the properties of this configuration and their proof using the following links.
Radical axis
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Let circles ![]() and
and ![]() be the circles with diameters
be the circles with diameters ![]() and
and ![]() respectively.
Prove that Steiner line
respectively.
Prove that Steiner line ![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
Proof
Let points ![]() and
and ![]() be the foots of perpendiculars
be the foots of perpendiculars ![]() and
and ![]() respectively.
respectively.
Denote ![]() power of point
power of point ![]() with respect the circle
with respect the circle ![]()
![]()
![]()
![]()
![]()
![]()
![]() Therefore power of points
Therefore power of points ![]() and
and ![]() with respect these three circles are the same, these points lies on the common radical axis of
with respect these three circles are the same, these points lies on the common radical axis of ![]() and
and ![]() Steiner line
Steiner line ![]() is the radical axis as desired.
is the radical axis as desired.