Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Complete Quadrilateral"

(→‎Newton–Gauss line)
(→‎Shatunov line)
Line 68: Line 68:
  
 
I suppose that this line was found by a young mathematician Leonid Shatunov in November 2020. I would be grateful for information on whether this line was previously known.
 
I suppose that this line was found by a young mathematician Leonid Shatunov in November 2020. I would be grateful for information on whether this line was previously known.
 +
 +
<i><b>Proof</b></i>
 +
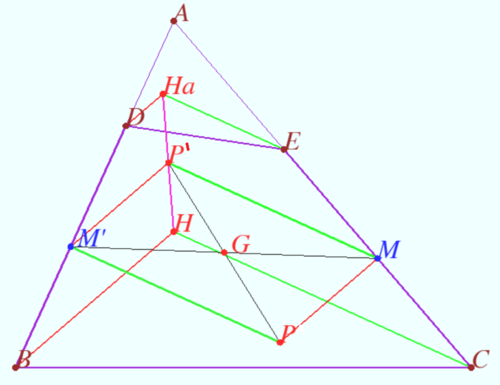
[[File:Shatunov line 2.png|500px|right]]
 +
a) Points <math>P</math> and <math>O</math> lies on bisector of <math>BC,</math> points <math>P</math> and <math>O_A</math> lies on bisector of <math>DE \implies</math>
 +
 +
<math>\angle OPO_A + \angle OO_CO_A = 180^\circ \implies P \in </math> circle <math>OO_AO_C.</math>
 +
 +
Similarly <math>P \in </math> circle <math>OO_BO_C</math> as desired.
 +
*[[Miquel's point]]
 +
 +
b) Let <math>M, M', P'</math> and <math>G</math> be midpoints of <math>CE, BD, HH_A,</math> and <math>MM',</math> respectively.
 +
 +
It is clear that <math>G</math> is centroid of <math>BDEC.</math>
 +
 +
<math>M'P \perp BD, EH_A \perp AD, CH \perp AB \implies MP' \perp AB</math> (midline of trapezium <math>ECHH_A) \implies EH_A||MP'||CH||M'P.</math>
 +
<cmath>MP \perp CE, DH_A \perp AE, BH \perp AC \implies</cmath>
 +
<math>M'P' \perp AB</math> (midline of trapezium <math>HBDH_A) \implies</math>
 +
<math>DH_A||M'P'||BH||MP \implies M'P'MP</math> is parallelogram.
 +
 +
Similarly one can prove that point <math>Q',</math> the midpoint of <math>H_BH_C,</math> is symmetric to <math>Q</math> with respect <math>G.</math>
 +
 +
Therefore line <math>P'Q'</math> coincide with Steiner line and line <math>PQ</math> is symmetric to Steiner line with respect <math>G</math> and is parallel to this line.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 09:03, 13 December 2022

Complete quadrilateral

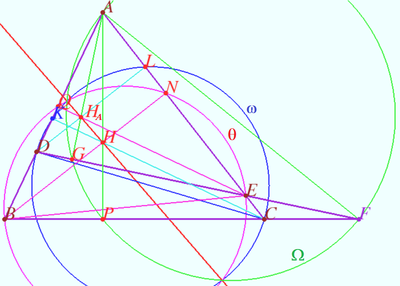
Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$ One can see some of the properties of this configuration and their proof using the following links.

Radical axis

Complete radical axes.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $H,$ and $H_A$ be the orthocenters of $\triangle ABC$ and $\triangle ADE,$ respectively.

Let circles $\omega, \theta,$ and $\Omega$ be the circles with diameters $CD, BE,$ and $AF,$ respectively. Prove that Steiner line $HH_A$ is the radical axis of $\omega, \theta,$ and $\Omega.$

Proof

Let points $G, K, L, N, P,$ and $Q$ be the foots of perpendiculars $AH_A, CH, DH_A, BH, AH,$ and $EH_A,$ respectively.

Denote $Po(X)_{\omega}$ power of point $X$ with respect the circle $\omega.$ \[\angle AGF = 90^\circ \implies G \in \Omega \implies Po(H_A)_{\Omega} = AH_A \cdot GH_A.\] \[\angle APF = 90^\circ \implies P \in \Omega \implies Po(H)_{\Omega} = AH \cdot PH_A.\] \[\angle CLD = 90^\circ \implies L \in \omega \implies Po(H_A)_{\omega} = DH_A \cdot LH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.\] \[\angle EQB = 90^\circ \implies Q \in \theta \implies Po(H_A)_{\theta} = EH_A \cdot QH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.\]

\[\angle BNE = 90^\circ \implies N \in \theta \implies Po(H)_{\theta} = BH \cdot NH = AH \cdot PH = Po(H)_{\Omega}.\] \[\angle CKD = 90^\circ \implies K \in \theta \implies Po(H)_{\omega} = CH \cdot KH = AH \cdot PH = Po(H)_{\Omega}.\] Therefore power of point $H (H_A)$ with respect these three circles is the same. These points lies on the common radical axis of $\omega, \theta,$ and $\Omega \implies$ Steiner line $HH_A$ is the radical axis as desired.

vladimir.shelomovskii@gmail.com, vvsss

Newton–Gauss line

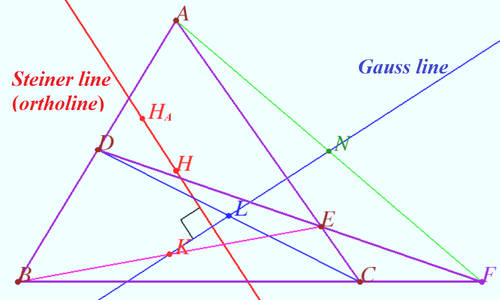
Complete perpendicular.png

Let four lines made four triangles of a complete quadrilateral.

In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $K, L,$ and $N$ be the midpoints of $BE, CD,$ and $AF,$ respectively.

Let points $H$ and $H_A$ be the orthocenters of $\triangle ABC$ and $\triangle ADE,$ respectively.

Prove that Steiner line $HH_A$ is perpendicular to Gauss line $KLN.$

Proof

Points $K, L,$ and $N$ are the centers of circles with diameters $BE, CD,$ and $AF,$ respectively.

Steiner line $HH_A$ is the radical axis of these circles.

Therefore $HH_A \perp KL$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

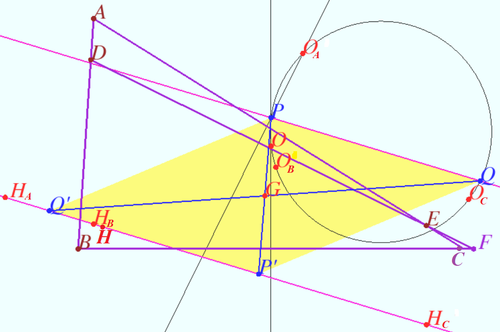
Shatunov line

Shatunov line 3.png

Let the complete quadrilateral ABCDEF be labeled as in the diagram.

Let points $H, H_A, H_B, H_C$ be the orthocenters and points $O, O_A, O_B, O_C$ be the circumcenters of $\triangle ABC, \triangle ADE, \triangle BDF,$ and $\triangle CEF,$ respectively.

Let bisector $BD$ cross bisector $CE$ at point $Q.$ Let bisector $BC$ cross bisector $DE$ at point $P.$

Prove that

a) points $P$ and $Q$ lie on circumcircle of $\triangle OO_AO_C,$

b) line $PQ$ is symmetric to Steiner line with respect centroid of $BDEC.$

I suppose that this line was found by a young mathematician Leonid Shatunov in November 2020. I would be grateful for information on whether this line was previously known.

Proof

Shatunov line 2.png

a) Points $P$ and $O$ lies on bisector of $BC,$ points $P$ and $O_A$ lies on bisector of $DE \implies$

$\angle OPO_A + \angle OO_CO_A = 180^\circ \implies P \in$ circle $OO_AO_C.$

Similarly $P \in$ circle $OO_BO_C$ as desired.

b) Let $M, M', P'$ and $G$ be midpoints of $CE, BD, HH_A,$ and $MM',$ respectively.

It is clear that $G$ is centroid of $BDEC.$

$M'P \perp BD, EH_A \perp AD, CH \perp AB \implies MP' \perp AB$ (midline of trapezium $ECHH_A) \implies EH_A||MP'||CH||M'P.$ \[MP \perp CE, DH_A \perp AE, BH \perp AC \implies\] $M'P' \perp AB$ (midline of trapezium $HBDH_A) \implies$ $DH_A||M'P'||BH||MP \implies M'P'MP$ is parallelogram.

Similarly one can prove that point $Q',$ the midpoint of $H_BH_C,$ is symmetric to $Q$ with respect $G.$

Therefore line $P'Q'$ coincide with Steiner line and line $PQ$ is symmetric to Steiner line with respect $G$ and is parallel to this line.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Complete_Quadrilateral&oldid=183924"