Difference between revisions of "British Mathematical Olympiad"
(→21-th Mathematical Olympiad 1985 Problem 5) |
(→21-th Mathematical Olympiad 1985 Problem 5) |
||
| Line 34: | Line 34: | ||
If the sphere rotates around an axis <math>OB,</math> then point <math>A</math> moves along circle with axis <math>OB.</math> | If the sphere rotates around an axis <math>OB,</math> then point <math>A</math> moves along circle with axis <math>OB.</math> | ||
| + | [[File:British 1985.png|350px|right]] | ||
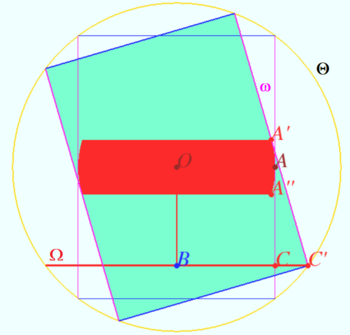
| + | Let the sphere rotates around an axis perpendicular <math>OA</math> and <math>OB.</math> | ||
| + | Axis view is shown on the diagram. We rotate <math>\Theta </math> together with <math>\omega</math> in counterclockwise direction. Point <math>C</math> moves along <math>\Omega</math> till point <math>C'</math> in the plane <math>OAB</math> where <math>\omega</math> touch <math>\Omega.</math> The point <math>A</math> moves to extreme position <math>A'.</math> | ||
| + | If one rotate <math>\Theta</math> in clockwise direction, point <math>A</math> moves to position <math>A''</math> symmetric to <math>A'</math> with respect <math>OA.</math> | ||
| + | <cmath>OA = OB = 3, BC' = A'C'= 4,</cmath> | ||
| + | <cmath>\angle A'C'B = 2 \arcsin \frac {3}{5} \implies</cmath> | ||
| + | <cmath>A'A'' = 2(\frac {96}{25} - 3) = \frac {42}{25} = 1.68.</cmath> | ||
| + | The locus of the point <math>A</math> is the belt with a width of <math>1.68</math> cm located on a sphere with a radius of <math>3</math> cm symmetrically to the circumference of the great circle located parallel hoop. | ||
| − | |||
| − | |||
| − | |||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 13:21, 18 May 2023
The British Mathematical Olympiad is a national math competition held in the United Kingdom. Solvers who score over a certain threshold in the Senior Mathematical Challenge are automatically entered to the first round, but others can register for the first round.
Contents
[hide]Structure
The British Mathematical Olympiad is divided into two rounds. In the first round (BMO 1), solvers have 3.5 hours to solve 6 problems. High scorers can move on into the second round (BMO 2), where solvers have 3.5 hours to solve 4 problems.
For both rounds, each problem is worth 10 points. Like most Olympiads, complete solutions are required in order to get full credit.
Participants who submit a solution with the highest quality in BMO 2 can earn the Christopher Bradley elegance prize.
Resources
21-th Mathematical Olympiad 1985 Problem 5
A circular hoop of radius 4 cm is held fixed in a horizontal plane. A cylinder with radius 4 cm and length 6 cm rests on the hoop with its axis horizontal, and with each of its two circular ends touching the hoop at two points. The cylinder is free to move subject to the condition that each of its circular ends always touches the hoop at two points. Find, with proof, the locus of the centre of one of the cylinder’s circular ends.
Solution
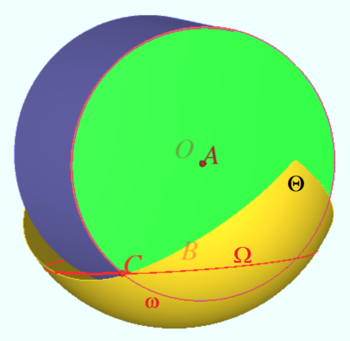
Let the centroid of the cylinder be the point ![]() The side surface of the cylinder is shown by dark blue.
The side surface of the cylinder is shown by dark blue.
Let the center of one of the circular ends be the point ![]() This end is shown by green. Its edge is a purple circle
This end is shown by green. Its edge is a purple circle ![]()
Let the center of the hoop ![]() be
be ![]() The hoop is shown by red.
The hoop is shown by red.
Let ![]() cross
cross ![]() at point
at point ![]() Therefore
Therefore ![]() cross
cross ![]() at second point symmetrical to
at second point symmetrical to ![]() with respect to the plane
with respect to the plane ![]()
![]() Let
Let ![]() be the sphere of radius
be the sphere of radius ![]() centered at
centered at ![]() Part of this sphere is shown in the diagram by yellow. Let the cylinder is glued to the sphere and point
Part of this sphere is shown in the diagram by yellow. Let the cylinder is glued to the sphere and point ![]() is fixed.
is fixed.
In this case ![]() and
and ![]() both lie on
both lie on ![]() and point
and point ![]() lies on the sphere centered at
lies on the sphere centered at ![]() with radius
with radius ![]()
The clime “The cylinder is free to move subject to the condition that each of its circular ends always touches the hoop at two points” has the equivalent form “The sphere is free to move with fixed center subject to the condition that ![]() cross
cross ![]() ”
”
If the sphere rotates around an axis ![]() then point
then point ![]() moves along circle with axis
moves along circle with axis ![]()
Let the sphere rotates around an axis perpendicular ![]() and
and ![]() Axis view is shown on the diagram. We rotate
Axis view is shown on the diagram. We rotate ![]() together with
together with ![]() in counterclockwise direction. Point
in counterclockwise direction. Point ![]() moves along
moves along ![]() till point
till point ![]() in the plane
in the plane ![]() where
where ![]() touch
touch ![]() The point
The point ![]() moves to extreme position
moves to extreme position ![]()
If one rotate ![]() in clockwise direction, point
in clockwise direction, point ![]() moves to position
moves to position ![]() symmetric to
symmetric to ![]() with respect
with respect ![]()
![]()
![]()
![]() The locus of the point
The locus of the point ![]() is the belt with a width of
is the belt with a width of ![]() cm located on a sphere with a radius of
cm located on a sphere with a radius of ![]() cm symmetrically to the circumference of the great circle located parallel hoop.
cm symmetrically to the circumference of the great circle located parallel hoop.
vladimir.shelomovskii@gmail.com, vvsss
Comments
This article is a stub. Help us out by expanding it.