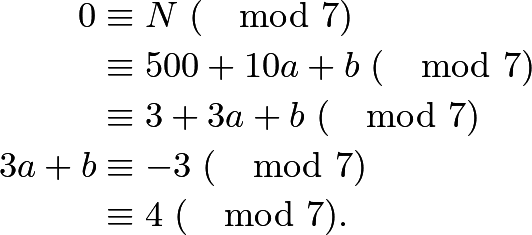Difference between revisions of "2023 AMC 10A Problems/Problem 12"
Technodoggo (talk | contribs) |
Technodoggo (talk | contribs) (→Solution 2 (solution 1 but more thorough + alternate way)) |
||
| Line 22: | Line 22: | ||
We then use modular arithmetic: | We then use modular arithmetic: | ||
| − | + | [[Image:2023_10a_12.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
We know that <math>0\le a,b<10</math>. We then look at each possible value of <math>a</math>: | We know that <math>0\le a,b<10</math>. We then look at each possible value of <math>a</math>: | ||
Revision as of 19:38, 9 November 2023
How many three-digit positive integers ![]() satisfy the following properties?
satisfy the following properties?
- The number
 is divisible by
is divisible by  .
.
- The number formed by reversing the digits of
 is divisble by
is divisble by  .
.
Solution 1
Multiples of 5 always end in 0 or 5 and since it is a three digit number, it cannot start with 0. All possibilities have to be in the range from 7 x 72 to 7 x 85 inclusive. 85 - 72 + 1 = 14. ![]() .
.
~walmartbrian ~Shontai ~andliu766
Solution 2 (solution 1 but more thorough + alternate way)
Let ![]() We know that
We know that ![]() is divisible by
is divisible by ![]() , so
, so ![]() is either
is either ![]() or
or ![]() . However, since
. However, since ![]() is the first digit of the three-digit number
is the first digit of the three-digit number ![]() , it can not be
, it can not be ![]() , so therefore,
, so therefore, ![]() . Thus,
. Thus, ![]() There are no further restrictions on digits
There are no further restrictions on digits ![]() and
and ![]() aside from
aside from ![]() being divisible by
being divisible by ![]() .
.
The smallest possible ![]() is
is ![]() . The next smallest
. The next smallest ![]() is
is ![]() , then
, then ![]() , and so on, all the way up to
, and so on, all the way up to ![]() . Thus, our set of possible
. Thus, our set of possible ![]() is
is ![]() . Dividing by
. Dividing by ![]() for each of the terms will not affect the cardinality of this set, so we do so and get
for each of the terms will not affect the cardinality of this set, so we do so and get ![]() . We subtract
. We subtract ![]() from each of the terms, again leaving the cardinality unchanged. We end up with
from each of the terms, again leaving the cardinality unchanged. We end up with ![]() , which has a cardinality of
, which has a cardinality of ![]() . Therefore, our answer is
. Therefore, our answer is ![]()
Alternate solution:
We first proceed as in the above solution, up to ![]() .
We then use modular arithmetic:
.
We then use modular arithmetic:
We know that ![]() . We then look at each possible value of
. We then look at each possible value of ![]() :
:
If ![]() , then
, then ![]() must be
must be ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() or
or ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() or
or ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() or
or ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() or
or ![]() .
.
If ![]() , then
, then ![]() must be
must be ![]() .
.
Each of these cases are unique, so there are a total of ![]()