Difference between revisions of "1992 OIM Problems/Problem 2"
| Line 9: | Line 9: | ||
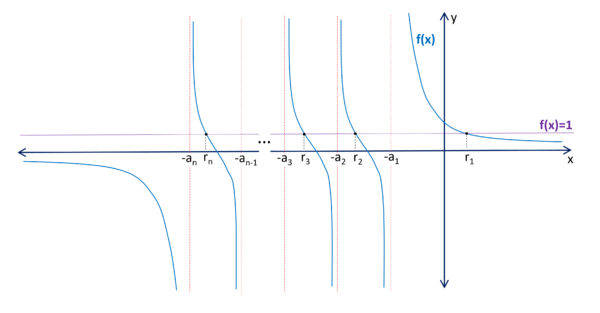
== Solution == | == Solution == | ||
| − | [[File: | + | [[File:1992_OIM_P2a.png|center|600px]] |
* Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later. | * Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later. | ||
Revision as of 10:57, 17 December 2023
Problem
Given the collection of 
positive real numbers 
and the function:
![\[f(x) = \frac{a_1}{x+a_1}+\frac{a_2}{x+a_2}+\cdots +\frac{a_n}{x+a_n}\]](http://latex.artofproblemsolving.com/b/d/b/bdb3b28e005214b8b860c79ba8f7995604c9b6d3.png)
Determine the sum of the lengths of the intervals, disjoint two by two, formed by all 
.
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
- Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got a ZERO on this one because I didn't even know what was I supposed to do, nor did I know what the sum of the lengths of the intervals, disjoint two by two meant. A decade ago I finally solved it but now I don't remember how. I will attempt to solve this one later.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
