Difference between revisions of "Cyclic quadrilateral"
(→Properties) |
Marianasinta (talk | contribs) |
||
| Line 13: | Line 13: | ||
* <math>\angle CAD = \angle CBD</math> | * <math>\angle CAD = \angle CBD</math> | ||
* All four [[perpendicular bisector|perpendicular bisectors]] are [[concurrent]]. The converse is also true. This intersection is the [[circumcenter]] of the quadrilateral. | * All four [[perpendicular bisector|perpendicular bisectors]] are [[concurrent]]. The converse is also true. This intersection is the [[circumcenter]] of the quadrilateral. | ||
| − | * Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites. | + | * Any two opposite sites of the quadrilateral are antiparallel with respect [https://artofproblemsolving.com/wiki/index.php/TOTO_SLOT_:_SITUS_TOTO_SLOT_MAXWIN_TERBAIK_DAN_TERPERCAYA TOTO SLOT] to the other two opposite sites. |
*ef=ac+bd (e and f are the diagonals) | *ef=ac+bd (e and f are the diagonals) | ||
Revision as of 15:59, 19 February 2024
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. While all triangles are cyclic, the same is not true of quadrilaterals. They have a number of interesting properties.
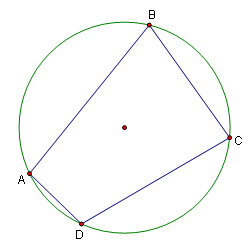
Properties
In a quadrilateral 
:
This property is both sufficient and necessary, and is often used to show that a quadrilateral is cyclic.
- All four perpendicular bisectors are concurrent. The converse is also true. This intersection is the circumcenter of the quadrilateral.
- Any two opposite sites of the quadrilateral are antiparallel with respect TOTO SLOT to the other two opposite sites.
- ef=ac+bd (e and f are the diagonals)
This property is both sufficient and necessary, and is often used to show that a quadrilateral is cyclic.
Applicable Theorems/Formulae
The following theorems and formulae apply to cyclic quadrilaterals:
This article is a stub. Help us out by expanding it.
