Difference between revisions of "Directed angles"

Revision as of 19:33, 25 December 2024

Directed Angles is a method to express angles that can be very useful in angle chasing problems where there are configuration issues.

Definition

Given any two non-parallel lines $l$ and $m$ , the directed angle $\measuredangle(l,m)$ is defined as the measure of the angle starting from $l$ and ending at $m$ , measured counterclockwise and modulo $180^{\circ}$ (or say it is modulo $\pi$ ). With this definition in place, we can define $\measuredangle AOB = \measuredangle(AO,BO)$ , where $AO$ and $BO$ are lines (rather than segments).

An equivalent statement for $\measuredangle AOB$ is that, $\measuredangle AOB$ is positive if the vertices $A$ , $B$ , $C$ appear in clockwise order, and negative otherwise, then we take the angles modulo $180^{\circ}$ (or modulo $\pi$ ).

Figure 1: The directed angle $\measuredangle(l,m)=50^{\circ}$ , while the directed angle $\measuredangle(m,l)=-50^{\circ}=130^{\circ}$

Figure 2: Here, $\measuredangle ABC=50^{\circ}$ and $\measuredangle CBA=-50^{\circ}=130^{\circ}$

Note that in some other places, regular $\angle$ notation is also used for directed angles. Some writers will also use $\equiv$ sign instead of a regular equal sign to indicate this modulo $180^{\circ}$ nature of a directed angle.

Warning

The notation introduced in this page for directed angles is still not very well known and standard. It is recommended by many educators that in a solution, it is needed to explicitly state the usage of directed angles.

Never take a half of a directed angle. Since directed angles are modulo $180^{\circ}$ , taking half of a directed angle may cause unexpected problems.

Do not use directed angles when the problem only works for a certain configuration.

Important Properties

Oblivion: $\measuredangle APA = 0$ .
Anti-Reflexivity: $\measuredangle ABC = -\measuredangle CBA$ .
Replacement: $\measuredangle PBA = \measuredangle PBC$ if and only if $A$ , $B$ , $C$ are collinear.
Right Angles: If $AP \perp BP$ , then $\measuredangle APB = \measuredangle BPA = 90^{\circ}$ .
Addition: $\measuredangle APB + \measuredangle BPC = \measuredangle APC$ .
Triangle Sum: $\measuredangle ABC + \measuredangle BCA + \measuredangle CAB = 0$ .
Isosceles Triangles: $AB = AC$ if and only if $\measuredangle ACB = \measuredangle CBA$ .
Inscribed Angle Theorem: If points $A$ , $B$ , $C$ is on a circle with center $P$ , then $\measuredangle APB = 2\measuredangle ACB$ .
Parallel Lines: If $AB \parallel CD$ , then $\measuredangle ABC + \measuredangle BCD = 0$ .
Cyclic Quadrilateral: Points $A$ , $B$ , $X$ , $Y$ lie on a circle if and only if $\measuredangle AXB = \measuredangle AYB$ .

Application

The slope of a line in a coordinate system can be given as the tangent of the directed angle between $x$ -axis and this line. (Remember the tangent function has a period $\pi$ , so we have our "modulo $\pi$ " part in tangent function)

Other than that, direct angles can be very useful when a geometric (usually angle chasing) problem have a lot of configuration issues. We can avoid solving the same problem twice (sometimes even multiple times) by applying direct angles.

Here are some examples with directed angles:

@@ Line 1: / Line 1: @@
-Skibidi
+'''Directed Angles''' is a method to express [[angles]] that can be very useful in angle chasing problems where there are configuration issues.
+== Definition ==
+Given any two non-parallel lines <math>l</math> and <math>m</math>, the '''directed angle''' <math>\measuredangle(l,m)</math> is defined as the measure of the angle '''starting''' from <math>l</math> and '''ending''' at <math>m</math>, measured '''counterclockwise''' and '''modulo <math>180^{\circ}</math> (or say it is modulo <math>\pi</math>)'''. With this definition in place, we can define <math>\measuredangle AOB = \measuredangle(AO,BO)</math>, where <math>AO</math> and <math>BO</math> are lines (rather than segments).
+An equivalent statement for <math>\measuredangle AOB</math> is that, <math>\measuredangle AOB</math> is '''positive''' if the vertices <math>A</math>, <math>B</math>, <math>C</math> appear in clockwise order, and '''negative''' otherwise, then we take the angles modulo <math>180^{\circ}</math> (or modulo <math>\pi</math>).
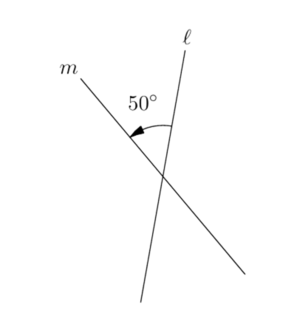
+[[IMage:50_deg_angle_l_m.png|thumb|Figure 1: The directed angle <math>\measuredangle(l,m)=50^{\circ}</math>, while the directed angle <math>\measuredangle(m,l)=-50^{\circ}=130^{\circ}</math>]]
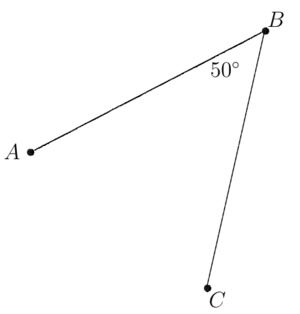
+[[IMage:50_deg_angle_ABC.png|thumb|Figure 2: Here, <math>\measuredangle ABC=50^{\circ}</math> and <math>\measuredangle CBA=-50^{\circ}=130^{\circ}</math>]]
+Note that in some other places, regular <math>\angle</math> notation is also used for directed angles. Some writers will also use <math>\equiv</math> sign instead of a regular equal sign to indicate this modulo <math>180^{\circ}</math> nature of a directed angle.
+== Warning ==
+* The notation introduced in this page for directed angles is still not very well known and standard. It is recommended by many educators that in a solution, it is needed to explicitly state the usage of directed angles.
+* Never take a half of a directed angle. Since directed angles are modulo <math>180^{\circ}</math>, taking half of a directed angle may cause unexpected problems.
+* Do not use directed angles when the problem only works for a '''certain''' configuration.
+== Important Properties ==
+* '''Oblivion''': <math>\measuredangle APA = 0</math>.
+* '''Anti-Reflexivity''': <math>\measuredangle ABC = -\measuredangle CBA</math>.
+* '''Replacement''': <math>\measuredangle PBA = \measuredangle PBC</math> if and only if <math>A</math>, <math>B</math>, <math>C</math> are collinear.
+* '''Right Angles''': If <math>AP \perp BP</math>, then <math>\measuredangle APB = \measuredangle BPA = 90^{\circ}</math>.
+* '''Addition''': <math>\measuredangle APB + \measuredangle BPC = \measuredangle APC</math>.
+* '''Triangle Sum''': <math>\measuredangle ABC + \measuredangle BCA + \measuredangle CAB = 0</math>.
+* '''Isosceles Triangles''': <math>AB = AC</math> if and only if <math>\measuredangle ACB = \measuredangle CBA</math>.
+* '''Inscribed Angle Theorem''': If points <math>A</math>, <math>B</math>, <math>C</math> is on a [[circle]] with [[center]] <math>P</math>, then <math>\measuredangle APB = 2\measuredangle ACB</math>.
+* '''Parallel Lines''': If <math>AB \parallel CD</math>, then <math>\measuredangle ABC + \measuredangle BCD = 0</math>.
+* '''[[Cyclic Quadrilateral]]''': Points <math>A</math>, <math>B</math>, <math>X</math>, <math>Y</math> lie on a circle if and only if <math>\measuredangle AXB = \measuredangle AYB</math>.
+== Application ==
+The [[slope]] of a line in a [[coordinate system]] can be given as the tangent of the directed angle between <math>x</math>-axis and this line. (Remember the tangent function has a period <math>\pi</math>, so we have our "modulo <math>\pi</math>" part in tangent function)
+Other than that, direct angles can be very useful when a geometric (usually angle chasing) problem have a lot of configuration issues. We can avoid solving the same problem twice (sometimes even multiple times) by applying direct angles.
+Here are some examples with directed angles:
+* Proof of the [[Miquel's_point|Miquel's Point]]
+* Proof of the [[Orthic_triangle|Orthic Triangle]]
+* Proof of the [[Pascal's Theorem]]
+* [[2002_IMO_Shortlist_Problems/G4|2002 IMO Shortlist Problems G4]]
+* [[2010_IMO_Shortlist_Problems/G1|2010 IMO Shortlist Problems G1]]
+* [[1998_APMO_Problems/Problem_4|1998 APMO Problem 4]]
+== See Also ==
+* [https://web.evanchen.cc/handouts/Directed-Angles/Directed-Angles.pdf Handout on Evan Chen's Website]
+* [https://www.math.ubbcluj.ro/~didactica/pdfs/2018/didmath2018-03.pdf An article on a Romanian Mathematical Journal, DIDACTICA MATHEMATICA]

Page

Toolbox

Search