Difference between revisions of "2005 AMC 10A Problems/Problem 8"
(→Solution) |
(→Solution) |
||
| Line 7: | Line 7: | ||
==Solution== | ==Solution== | ||
| − | We see that side <math>BE</math>, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, <math>AH = 1</math>. Then <math>HB = HE + BE = HE + 1</math>, and <math>HE</math> is one of the sides of the square whose area we want to find. So: | + | '''(B)''' We see that side <math>BE</math>, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, <math>AH = 1</math>. Then <math>HB = HE + BE = HE + 1</math>, and <math>HE</math> is one of the sides of the square whose area we want to find. So: |
<math>1^2 + (HE+1)^2=\sqrt{50}^2</math> | <math>1^2 + (HE+1)^2=\sqrt{50}^2</math> | ||
Revision as of 19:50, 30 January 2011
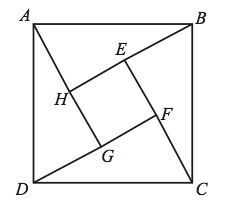
Problem
In the figure, the length of side ![]() of square
of square ![]() is
is ![]() and
and ![]() =1. What is the area of the inner square
=1. What is the area of the inner square ![]() ?
?
![]()
Solution
(B) We see that side ![]() , which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So,
, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, ![]() . Then
. Then ![]() , and
, and ![]() is one of the sides of the square whose area we want to find. So:
is one of the sides of the square whose area we want to find. So:
![]()
![]()
![]()
![]()
![]() So, the area of the square is
So, the area of the square is ![]() .
.