Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 10A Problems/Problem 19"
Line 2: Line 2:
  
 
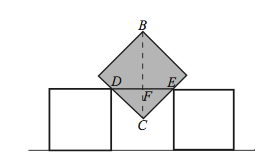
Then you have to add the 1 from the height of the other two squares, so you get <math>1+BF=\sqrt{2}+\dfrac{1}{2}</math>.
 
Then you have to add the 1 from the height of the other two squares, so you get <math>1+BF=\sqrt{2}+\dfrac{1}{2}</math>.
 +
 +
[[File:AMC10200519Sol.png]]

Revision as of 20:29, 30 January 2011

(D) Consider the rotated middle square shown in the figure. It will drop until length $DE$ is 1 inch. Thus $FC=DF=FE=\dfrac{1}{2}$ and $BC=\sqrt{2}$. Hence, $BF=BC-FC=\sqrt{2}-\dfrac{1}{2}$.

Then you have to add the 1 from the height of the other two squares, so you get $1+BF=\sqrt{2}+\dfrac{1}{2}$.

AMC10200519Sol.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_19&oldid=36528"