Difference between revisions of "Squeeze Theorem"
Pi3point14 (talk | contribs) (→Applications and examples) |
Pi3point14 (talk | contribs) (→Applications and examples) |
||
| Line 22: | Line 22: | ||
== Applications and examples== | == Applications and examples== | ||
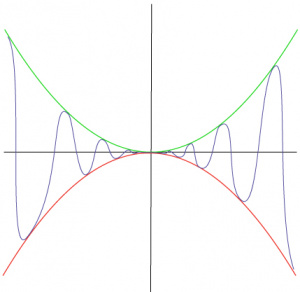
| − | The Squeeze Theorem can be used to evaluate limits that might not normally be defined. An example is the | + | The Squeeze Theorem can be used to evaluate limits that might not normally be defined. An example is the function <math>f(x)=x^2 e^{\sin\frac{1}{x}}</math> with thelimit <math>\lim_{x\to\0} f(x)=x^2 e^{\sin\frac{1}{x}}</math>. The limit is not normally defined, because the function oscillates infinitely many times around 0, but it can be evaluated with the Squeeze Theorem as following. Create two functions, <math>x^2</math> and <math>-x^2</math>. It is easy to see that around 0, the function in question is squeezed between these two functions, and the limit as both of these approach 0 is 0, so <math>\lim_{x\to\0} x^2 e^{\sin\frac{1}{x}}</math> is 0. |
Revision as of 21:14, 28 August 2015
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Contents
[hide]Theorem
Suppose ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in a neighborhood of the point
in a neighborhood of the point ![]() . If
. If ![]() and
and ![]() approach some common limit
approach some common limit ![]() as
as ![]() approaches
approaches ![]() , then
, then ![]() .
.
Proof
If ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() , then either
, then either ![]() or
or ![]() for all
for all ![]() in this neighborhood. The two cases are the same up to renaming our functions, so assume without loss of generality that
in this neighborhood. The two cases are the same up to renaming our functions, so assume without loss of generality that ![]() .
.
We must show that for all ![]() there is some
there is some ![]() for which
for which ![]() implies
implies ![]() .
.
Now since ![]() , there must exist
, there must exist ![]() such that
such that
![]()
Now let ![]() . If
. If ![]() then
then
![]()
So ![]() . Now by the definition of a limit we get
. Now by the definition of a limit we get ![]() as desired.
as desired.
Applications and examples
The Squeeze Theorem can be used to evaluate limits that might not normally be defined. An example is the function ![]() with thelimit $\lim_{x\to\0} f(x)=x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg). The limit is not normally defined, because the function oscillates infinitely many times around 0, but it can be evaluated with the Squeeze Theorem as following. Create two functions,
with thelimit $\lim_{x\to\0} f(x)=x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg). The limit is not normally defined, because the function oscillates infinitely many times around 0, but it can be evaluated with the Squeeze Theorem as following. Create two functions, ![]() and
and ![]() . It is easy to see that around 0, the function in question is squeezed between these two functions, and the limit as both of these approach 0 is 0, so $\lim_{x\to\0} x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg) is 0.
. It is easy to see that around 0, the function in question is squeezed between these two functions, and the limit as both of these approach 0 is 0, so $\lim_{x\to\0} x^2 e^{\sin\frac{1}{x}}$ (Error compiling LaTeX. Unknown error_msg) is 0.