Difference between revisions of "2006 AMC 10B Problems/Problem 6"
Ragnarok23 (talk | contribs) |
(Added problem and solution) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
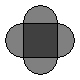
| + | A region is bounded by semicircular arcs constructed on the side of a square whose sides measure <math> \frac{2}{\pi} </math>, as shown. What is the perimeter of this region? | ||
| + | |||
| + | [[Image:2006amc10b06.gif]] | ||
| + | |||
| + | <math> \mathrm{(A) \ } \frac{4}{\pi}\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } \frac{8}{\pi}\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } \frac{16}{\pi} </math> | ||
| + | |||
== Solution == | == Solution == | ||
| + | Since the side of the square is the diameter of the semicircle, the radius of the semicircle is <math> \frac{1}{2}\cdot\frac{2}{\pi}=\frac{1}{\pi} </math> | ||
| + | |||
| + | Since the length of one of the semicircular arcs is half the circumference of the corresponding circle, the length of one arc is <math> \frac{1}{2}\cdot2\cdot\pi\cdot\frac{1}{\pi}=1</math> | ||
| + | |||
| + | Since the desired perimeter is made up of four of these arcs, the perimeter is <math>4\cdot1=4\Rightarrow D</math> | ||
| + | |||
== See Also == | == See Also == | ||
*[[2006 AMC 10B Problems]] | *[[2006 AMC 10B Problems]] | ||
Revision as of 19:37, 13 July 2006
Problem
A region is bounded by semicircular arcs constructed on the side of a square whose sides measure 
, as shown. What is the perimeter of this region?
Solution
Since the side of the square is the diameter of the semicircle, the radius of the semicircle is 
Since the length of one of the semicircular arcs is half the circumference of the corresponding circle, the length of one arc is 
Since the desired perimeter is made up of four of these arcs, the perimeter is 
