Difference between revisions of "2006 AMC 10B Problems/Problem 15"
Ragnarok23 (talk | contribs) |
(Added problem and solution) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
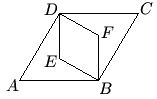
| + | Rhombus <math>ABCD</math> is similar to rhombus <math>BFDE</math>. The area of rhombus <math>ABCD</math> is <math>24</math> and <math> \angle BAD = 60^\circ </math>. What is the area of rhombus <math>BFDE</math>? | ||
| + | |||
| + | [[Image:2006amc10b15.gif]] | ||
| + | |||
| + | <math> \mathrm{(A) \ } 6\qquad \mathrm{(B) \ } 4\sqrt{3}\qquad \mathrm{(C) \ } 8\qquad \mathrm{(D) \ } 9\qquad \mathrm{(E) \ } 6\sqrt{3} </math> | ||
| + | |||
== Solution == | == Solution == | ||
| + | Using properties of a [[rhombus]]: | ||
| + | |||
| + | <math> \angle DAB = \angle DCB = 60 ^\circ </math>. | ||
| + | |||
| + | <math> \angle ADC = \angle ABC = 120 ^\circ </math>. | ||
| + | |||
| + | It is easy to see that rhombus <math>ABCD</math> is made up of equilateral triangles <math>DAB</math> and <math>DCB</math>. | ||
| + | |||
| + | Let the lengths of the sides of rhombus <math>ABCD</math> be <math>s</math>. | ||
| + | |||
| + | The longer diagonal of rhombus <math>BFDE</math> is <math>BD</math>. Since <math>BD</math> is a side of an equilateral triangle with a side length of <math>s</math>, <math> BD = s </math>. | ||
| + | |||
| + | The longer diagonal of rhombus <math>ABCD</math> is <math>AC</math>. Since <math>AC</math> is twice the length of an altitude of of an equilateral triangle with a side length of <math>s</math>, <math> AC = 2 \cdot \frac{s\sqrt{3}}{2} = s\sqrt{3} </math> | ||
| + | |||
| + | The ratio of the longer diagonal of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \frac{s}{s\sqrt{3}} = \frac{\sqrt{3}}{3} </math> | ||
| + | |||
| + | Therefore, the ratio of the area of rhombus <math>BFDE</math> to rhombus <math>ABCD</math> is <math> \left( \frac{\sqrt{3}}{3} \right) ^2 = \frac{1}{3} </math> | ||
| + | |||
| + | Let <math>x</math> be the area of rhombus <math>BFDE</math>. | ||
| + | |||
| + | <math> \frac{x}{24} = \frac{1}{3} </math> | ||
| + | |||
| + | <math> x = 8 \Rightarrow C </math> | ||
| + | |||
== See Also == | == See Also == | ||
*[[2006 AMC 10B Problems]] | *[[2006 AMC 10B Problems]] | ||
Revision as of 15:24, 19 July 2006
Problem
Rhombus ![]() is similar to rhombus
is similar to rhombus ![]() . The area of rhombus
. The area of rhombus ![]() is
is ![]() and
and ![]() . What is the area of rhombus
. What is the area of rhombus ![]() ?
?
![]()
Solution
Using properties of a rhombus:
![]() .
.
![]() .
.
It is easy to see that rhombus ![]() is made up of equilateral triangles
is made up of equilateral triangles ![]() and
and ![]() .
.
Let the lengths of the sides of rhombus ![]() be
be ![]() .
.
The longer diagonal of rhombus ![]() is
is ![]() . Since
. Since ![]() is a side of an equilateral triangle with a side length of
is a side of an equilateral triangle with a side length of ![]() ,
, ![]() .
.
The longer diagonal of rhombus ![]() is
is ![]() . Since
. Since ![]() is twice the length of an altitude of of an equilateral triangle with a side length of
is twice the length of an altitude of of an equilateral triangle with a side length of ![]() ,
, ![]()
The ratio of the longer diagonal of rhombus ![]() to rhombus
to rhombus ![]() is
is ![]()
Therefore, the ratio of the area of rhombus ![]() to rhombus
to rhombus ![]() is
is 
Let ![]() be the area of rhombus
be the area of rhombus ![]() .
.
![]()
![]()