Difference between revisions of "2005 AMC 10A Problems/Problem 8"

Revision as of 15:15, 10 August 2017

Problem

In the figure, the length of side $AB$ of square $ABCD$ is $\sqrt{50}$ and $BE$ =1. What is the area of the inner square $EFGH$ ?

$\textbf{(A)}\ 25\qquad\textbf{(B)}\ 32\qquad\textbf{(C)}\ 36\qquad\textbf{(D)}\ 40\qquad\textbf{(E)}\ 42$

Solution

We see that side $BE$ , which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, $AH = 1$ . Then $HB = HE + BE = HE + 1$ , and $HE$ is one of the sides of the square whose area we want to find. So:

$1^2 + (HE+1)^2=\sqrt{50}^2$

$1 + (HE+1)^2=50$

$(HE+1)^2=49$

$HE+1=7$

$HE=6$ So, the area of the square is $6^2=\boxed{36} \Rightarrow \mathrm{(C)}$ .

@@ Line 25: / Line 25: @@
 [[Category:Area Problems]]
 {{MAA Notice}}
+*[[2005 AMC 10A Problems]]
+*[[2005 AMC 10A Problems/Problem 7|Previous Problem]]
+*[[2005 AMC 10A Problems/Problem 9|Next Problem]]

Page

Toolbox

Search

Difference between revisions of "2005 AMC 10A Problems/Problem 8"

Revision as of 15:15, 10 August 2017

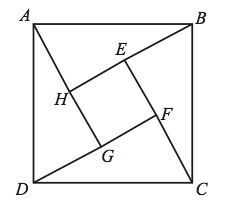
Problem

Solution

See Also