2019 IMO Problems/Problem 6
Problem
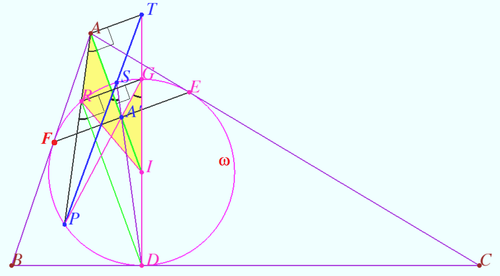
Let ![]() be the incenter of acute triangle
be the incenter of acute triangle ![]() with
with ![]() . The incircle
. The incircle ![]() of
of ![]() is tangent to sides
is tangent to sides ![]() ,
, ![]() , and
, and ![]() at
at ![]() ,
, ![]() , and
, and ![]() , respectively. The line through
, respectively. The line through ![]() perpendicular to
perpendicular to ![]() meets
meets ![]() again at
again at ![]() . Line
. Line ![]() meets ω again at
meets ω again at ![]() . The circumcircles of triangles
. The circumcircles of triangles ![]() and
and ![]() meet again at
meet again at ![]() .
Prove that lines
.
Prove that lines ![]() and
and ![]() meet on the line through
meet on the line through ![]() perpendicular to
perpendicular to ![]() .
.
Solution
Step 1
We find an auxiliary point ![]()
Let ![]() be the antipode of
be the antipode of ![]() on
on ![]() where
where ![]() is radius
is radius ![]()
We define ![]()
![]() cyclic
cyclic ![]()
![]() an inversion with respect
an inversion with respect ![]() swap
swap ![]() and
and ![]() is the midpoint
is the midpoint ![]() Let
Let ![]() meets
meets ![]() again at S (other than D). We define
again at S (other than D). We define ![]() Opposite sides of any quadrilateral inscribed in the circle
Opposite sides of any quadrilateral inscribed in the circle ![]() meet on the polar line of the intersection of the diagonals with respect to
meet on the polar line of the intersection of the diagonals with respect to ![]() and
and ![]() meet on the line through
meet on the line through ![]() perpendicular to
perpendicular to ![]() The problem is reduced to proving that
The problem is reduced to proving that ![]()