2021 Fall AMC 10B Problems/Problem 23
Problem
Each of the ![]() sides and the
sides and the ![]() diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability. What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color?
diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability. What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color?
![]()
Solution 1
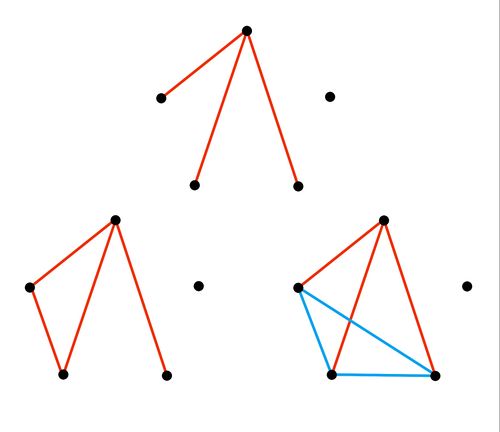
Instead of finding the probability of a same-colored triangle appearing, let us find the probability that one does not appear. After drawing the regular pentagon out, note the topmost vertex; it has 4 sides/diagonals emanating outward from it. We do casework on the color distribution of these sides/diagonals.
![]() : all 4 are colored one color. In that case, all of the remaining sides must be of the other color to not have a triangle where all three sides are of the same color. We can correspondingly fill out each color based on this constraint, but in this case you will always end up with a triangle where all three sides have the same color by inspection.
: all 4 are colored one color. In that case, all of the remaining sides must be of the other color to not have a triangle where all three sides are of the same color. We can correspondingly fill out each color based on this constraint, but in this case you will always end up with a triangle where all three sides have the same color by inspection.
![]() : 3 are one color and one is the other. Following the steps from the previous case, you can try filling out the colors, but will always arrive at a contradiction so this case does not work either.
: 3 are one color and one is the other. Following the steps from the previous case, you can try filling out the colors, but will always arrive at a contradiction so this case does not work either.
![]() : 2 are one color and 2 are of the other color. Using the same logic as previously, we can color the pentagon 2 different ways by inspection to satisfy the requirements. There are
: 2 are one color and 2 are of the other color. Using the same logic as previously, we can color the pentagon 2 different ways by inspection to satisfy the requirements. There are ![]() ways to color the original sides/diagonals and 2 ways after that to color the remaining ones for a total of
ways to color the original sides/diagonals and 2 ways after that to color the remaining ones for a total of ![]() ways to color the pentagon so that no such triangle has the same color for all of its sides.
ways to color the pentagon so that no such triangle has the same color for all of its sides.
These are all the cases, and there are a total of ![]() ways to color the pentagon. Therefore the answer is
ways to color the pentagon. Therefore the answer is ![]()
~KingRavi
Solution 2 (Ramsey's Theorem)
This problem is related to a special case of Ramsey's Theorem, R(3, 3) = 6. Suppose we color every edge of a complete ![]() vertex graph
vertex graph ![]() with
with ![]() colors, there must exist a
colors, there must exist a ![]() vertex complete graph
vertex complete graph ![]() with all it's edges in the same color. That is,
with all it's edges in the same color. That is, ![]() contains a monochromatic
contains a monochromatic ![]() .
.
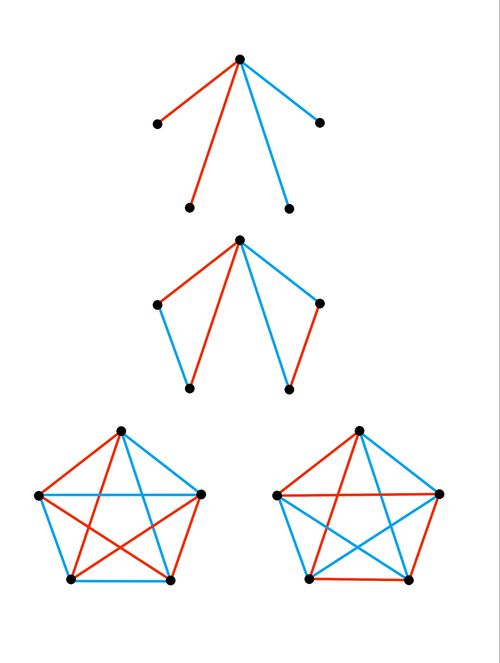
Choose a vertex, there will be ![]() edges radiating from it.
edges radiating from it.
Case 1: When ![]() or more edges are the same color, there must exist a monochromatic
or more edges are the same color, there must exist a monochromatic ![]() . It is shown below. Suppose the color is red. There must be a same colored triangle as shown in the diagram below.
. It is shown below. Suppose the color is red. There must be a same colored triangle as shown in the diagram below.
There is only ![]() way to color all the edges in the same color. There is
way to color all the edges in the same color. There is  ways to color
ways to color ![]() of the edges in the same color.
of the edges in the same color.
Case 2: When ![]() edges are the same color, there are many graphs that monochromatic
edges are the same color, there are many graphs that monochromatic ![]() and some that doesn't. I will count the number of graphs that doesn't contain a monochromatic
and some that doesn't. I will count the number of graphs that doesn't contain a monochromatic ![]() . Suppose the color is red, following steps in the diagram below there are
. Suppose the color is red, following steps in the diagram below there are ![]() graphs that doesn't contain a monochromatic
graphs that doesn't contain a monochromatic ![]() .
.
There is  ways to color the edges with
ways to color the edges with ![]() edges the same color. There are
edges the same color. There are ![]() graphs with the
graphs with the ![]() same colored edges arranged in the above diagram. So there is
same colored edges arranged in the above diagram. So there is ![]() graphs that contains a monochromatic
graphs that contains a monochromatic ![]() .
.
Case 4: When ![]() or less edges are the same color, it is the symmetrical to case 1.
or less edges are the same color, it is the symmetrical to case 1.
![]()
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.