2021 USAMO Problems/Problem 6
Problem 6
Let ![]() be a convex hexagon satisfying
be a convex hexagon satisfying ![]() ,
, ![]() ,
, ![]() , and
, and![]() Let
Let ![]() ,
, ![]() , and
, and ![]() be the midpoints of
be the midpoints of ![]() ,
, ![]() , and
, and ![]() . Prove that the circumcenter of
. Prove that the circumcenter of ![]() , the circumcenter of
, the circumcenter of ![]() , and the orthocenter of
, and the orthocenter of ![]() are collinear.
are collinear.
Solution
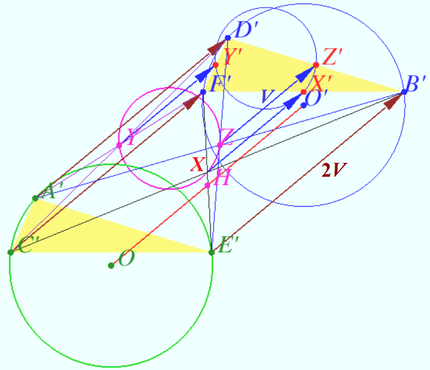
We construct two equal triangles, prove that triangle ![]() is the medial triangle of both this triangles, use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.
is the medial triangle of both this triangles, use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.
Denote ![]()
![]() Then
Then ![]() Denote
Denote ![]()
Symilarly we get ![]()
![]() and the translation vector is
and the translation vector is ![]()
![]()
so ![]() is midpoint of
is midpoint of ![]() and
and ![]() Symilarly
Symilarly ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() and
and ![]()
![]() is the midpoint of
is the midpoint of ![]() Symilarly
Symilarly ![]() is the midpoint of
is the midpoint of ![]() is the midpoint of
is the midpoint of ![]() so
so ![]() is the medial triangle of
is the medial triangle of ![]() translated on
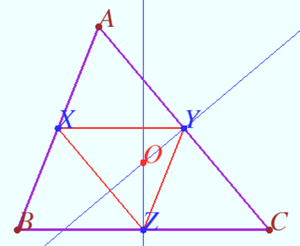
translated on ![]() It is known (see diagram) that circumcenter of triangle coincite with orthocenter of the medial triangle. Therefore orthocenter
It is known (see diagram) that circumcenter of triangle coincite with orthocenter of the medial triangle. Therefore orthocenter ![]() of
of ![]() is circumcenter of
is circumcenter of ![]() translated on
translated on ![]() It is the midpoint of segment
It is the midpoint of segment ![]() connected circumcenters of
connected circumcenters of ![]() and
and ![]()
According to the definition of points ![]() and
and ![]() are parallelograms
are parallelograms ![]()
![]()
![]() Power of points A,C, and E with respect circumcircle \triangle A'C'E' is equal, hence distances between these points and circumcenter of \triangle A'C'E' are the same \implies circumcenters of constructed triangles coincide with given circumcenters.
Power of points A,C, and E with respect circumcircle \triangle A'C'E' is equal, hence distances between these points and circumcenter of \triangle A'C'E' are the same \implies circumcenters of constructed triangles coincide with given circumcenters.