Miquel's point

Miquel and Steiner's quadrilateral theorem

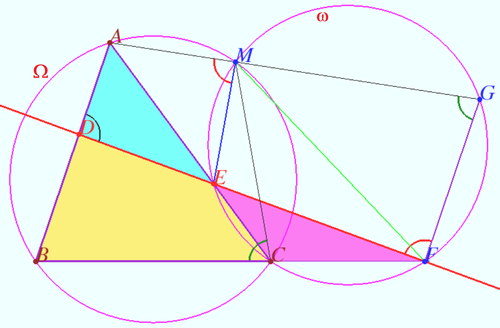
Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcircles of all four triangles meet at a single point.

Proof

Let circumcircle of $\triangle ABC$ circle $\Omega$ cross the circumcircle of $\triangle CEF$ circle $\omega$ at point $M.$

Let $AM$ cross $\omega$ second time in the point $G.$

$CMGF$ is cyclic $\implies \angle BCM = \angle MGF.$

$AMCB$ is cyclic $\implies \angle BCM + \angle BAM = 180^\circ \implies$

$\angle BAG + \angle AGF = 180^\circ \implies AB||GF.$

$CMGF$ is cyclic $\implies \angle AME = \angle EFG.$

$AD||GF \implies \angle ADE + \angle DFG = 180^\circ \implies \angle ADE + \angle AME = 180^\circ \implies$

$ADEM$ is cyclic and circumcircle of $\triangle ADE$ contain the point $M.$

Similarly circumcircle of $\triangle BDF$ contain the point $M$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Circle of circumcenters

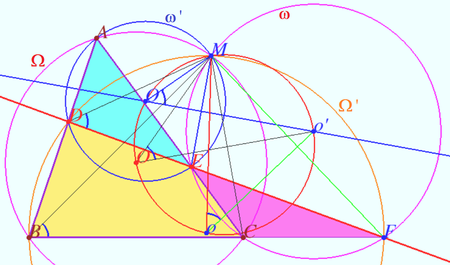
Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Prove that the circumcenters of all four triangles and point $M$ are concyclic.

Proof

Let $\Omega, \omega, \Omega',$ and $\omega'$ be the circumcircles of $\triangle ABC, \triangle CEF, \triangle BDF,$ and $\triangle ADE,$ respectively.

In $\Omega' \angle MDF = \angle MBF.$

In $\omega' \angle MDE = \frac {\overset{\Large\frown} {ME}} {2}.$

$ME$ is the common chord of $\omega$ and $\omega' \implies \angle MOE = \overset{\Large\frown} {ME} \implies$

$\angle MO'o' = \frac {\overset{\Large\frown} {ME}} {2} = \angle MDE.$

Similarly, $MF$ is the common chord of $\omega$ and $\Omega' \implies \angle MDF = \angle Moo' = \angle MO'o'.$

Similarly, $MC$ is the common chord of $\Omega$ and $\omega' \implies \angle MBC = \angle MOo' \implies$

$\angle MOo' = \angle MO'o' \implies$ points $M, O, O', o,$ and $o'$ are concyclic as desired.

vladimir.shelomovskii@gmail.com, vvsss

Triangle of circumcenters

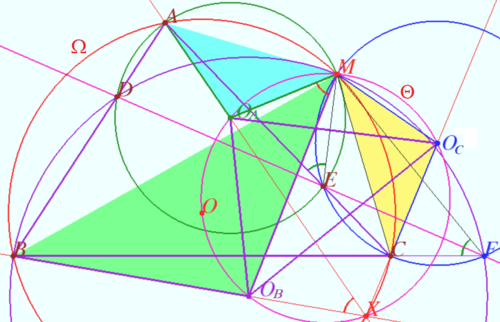
Let four lines made four triangles of a complete quadrilateral.

In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $O,O_A, O_B,$ and $O_C$ be the circumcenters of $\triangle ABC, \triangle ADE, \triangle BDF,$ and $\triangle CEF,$ respectively.

Prove that $\triangle O_AO_BO_C \sim \triangle ABC,$ and perspector of these triangles point $X$ is the second (different from $M$ ) point of intersection $\Omega \cap \Theta,$ where $\Omega$ is circumcircle of $\triangle ABC$ and $\Theta$ is circumcircle of $\triangle O_AO_BO_C.$

Proof

Quadrungle $MECF$ is cyclic $\implies \angle AEM = \angle BFM \implies$ $\angle AO_AB = 2\angle AEM = 2 \angle BFM = \angle BO_BM.$ $\angle CO_CM = 2\angle CFM = 2 \angle BFM = \angle BO_BM.$ $AO_A = MO_A, BO_B = MO_B, CO_C = MO_C \implies \triangle AO_AM \sim \triangle BO_BM \sim \triangle CO_CM.$

Spiral similarity sentered at point $M$ with rotation angle $\angle AMO_A = \angle BMO_B = CMO_C$ and the coefficient of homothety $\frac {AM}{MO_A} = \frac {BM}{MO_B} =\frac {CM}{MO_C}$ mapping $A$ to $O_A$ , $B$ to $O_B$ , $C$ to $O_C \implies \triangle O_AO_BO_C \sim \triangle ABC.$

$\triangle AO_AM, \triangle BO_BM, \triangle CO_CM$ are triangles in double perspective at point $M \implies$

these triangles are in triple perspective $\implies AO_A, BO_B, CO_C$ are concurrent at the point $X.$

The rotation angle $\triangle AO_AM$ to $\triangle BO_BM$ is $\angle O_AMO_B$ for sides $O_AM$ and $O_BM$ or angle between $AO_A$ and $BO_B$ which is $\angle AXB \implies M O_AO_BX$ is cyclic $\implies M O_AO_BXO_C$ is cyclic.