2003 USAMO Problems/Problem 4
Contents
[hide]Problem
Let ![]() be a triangle. A circle passing through
be a triangle. A circle passing through ![]() and
and ![]() intersects segments
intersects segments ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , while lines
, while lines ![]() and
and ![]() intersect at
intersect at ![]() . Prove that
. Prove that ![]() if and only if
if and only if ![]() .
.
Solutions
Solution 1
Extend segment ![]() through
through ![]() to
to ![]() such that
such that ![]() .
.
![[asy] defaultpen(fontsize(10)+0.6); size(250); var theta=22, r=0.58; pair B=origin, A=dir(theta), C=A+(rotate(78)*0.8*A), O=IP(CR(B,r),CR(A,r)); path c=CR(O,r); pair D=IP(c,A--C), E=IP(c,B--C), F=extension(A,B,D,E), M=extension(B,D,C,F), G=extension(D,M,F,F+C-D); draw(A--B--C--A^^E--F--C^^A--F^^B--M^^E--M); draw(c); draw(F--G--C^^M--G,gray+0.4); dot("$A$",A,dir(F-E)); dot("$B$",B,2*dir(B-A)); dot("$C$",C,1.5*dir(C-A)); dot("$D$",D,2.5*dir(250)); dot("$E$",E,2.5*dir(C-A)); dot("$F$",F,dir(F-E)); dot("$M$",M,2.5*dir(255)); dot("$G$",G,dir(G-M)); [/asy]](http://latex.artofproblemsolving.com/8/a/e/8aebb0446ff1f10ad418ae2cce5809fb8a1cd38d.png) Then
Then ![]() if and only if quadrilateral
if and only if quadrilateral ![]() is a parallelogram, or,
is a parallelogram, or, ![]() . Hence
. Hence ![]() if and only if
if and only if ![]() , that is,
, that is, ![]() .
.
Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . It follows that
. It follows that ![]() if and only if
if and only if
![]() that is, quadrilateral
that is, quadrilateral ![]() is cyclic, which is equivalent to
is cyclic, which is equivalent to
![]() Because
Because ![]() ,
, ![]() if and only if triangles
if and only if triangles ![]() and
and ![]() are similar, that is
are similar, that is
![]() or
or ![]() .
.
Solution 2
We first assume that ![]() . Because
. Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() . This exact condition can also be visualized through power of M with respect to the circumcircle of triangle
. This exact condition can also be visualized through power of M with respect to the circumcircle of triangle ![]() and getting the angle condition from the alternate segment theorem.
and getting the angle condition from the alternate segment theorem.
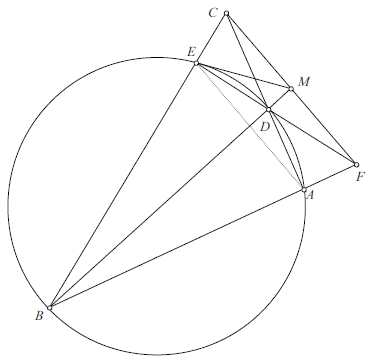
Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() implying that
implying that ![]() , so
, so ![]() . Because quadrilateral
. Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() Because
Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() , or
, or ![]() . Therefore
. Therefore ![]() implies
implies ![]() .
.
Now we assume that ![]() . Applying Ceva's Theorem to triangle
. Applying Ceva's Theorem to triangle ![]() and cevians
and cevians ![]() gives
gives
![]() implying that
implying that ![]() , so
, so ![]() .
.
Consequently, ![]() . Because quadrilateral
. Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() Because
Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() , or
, or ![]() .
.
Combining the above, we conclude that ![]() if and only if
if and only if ![]() .
.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See also
| 2003 USAMO (Problems • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









