Spiral similarity
Contents
[hide]Basic information
A spiral similarity is a plane transformation composed of a rotation of the plane and a dilation of the plane having the common center. The order in which the composition is taken is not important.
The transformation is linear and transforms any given object into an object homothetic to given.
On the complex plane, any spiral similarity can be expressed in the form ![]() where
where ![]() is a complex number. The magnitude
is a complex number. The magnitude ![]() is the dilation factor of the spiral similarity, and the argument
is the dilation factor of the spiral similarity, and the argument ![]() is the angle of rotation.
is the angle of rotation.
The spiral similarity is uniquely defined by the images of two distinct points. It is easy to show using the complex plane.
Let ![]() with corresponding complex numbers
with corresponding complex numbers ![]() and
and ![]() so
so
![]()
![]()
![]()
Case 1 Any line segment ![]() can be mapped into any other
can be mapped into any other ![]() using the spiral similarity. Notation is shown on the diagram.
using the spiral similarity. Notation is shown on the diagram.
![]()
![]() is circle
is circle ![]() is circle
is circle ![]()
![]() is any point of
is any point of ![]() is circle
is circle ![]() is the image
is the image ![]() under spiral symilarity centered at
under spiral symilarity centered at ![]()
![]()
![]() is the dilation factor,
is the dilation factor,
![]() is the angle of rotation.
is the angle of rotation.
Case 2 Any line segment ![]() can be mapped into any other
can be mapped into any other ![]() using the spiral similarity. Notation is shown on the diagram.
using the spiral similarity. Notation is shown on the diagram. ![]() is circle
is circle ![]() (so circle is tangent to
(so circle is tangent to ![]() is circle tangent to
is circle tangent to ![]() is any point of
is any point of ![]() is circle
is circle ![]()
![]() is the image
is the image ![]() under spiral symilarity centered at
under spiral symilarity centered at ![]()
![]()
![]() is the dilation factor,
is the dilation factor,
![]() is the angle of rotation.
is the angle of rotation.
Simple problems
Explicit spiral symilarity
Given two similar right triangles ![]() and
and ![]()
![]() Find
Find ![]() and
and ![]()
Solution
The spiral symilarity centered at ![]() with coefficient
with coefficient ![]() and the angle of rotation
and the angle of rotation ![]() maps point
maps point ![]() to point
to point ![]() and point
and point ![]() to point
to point ![]()
Therefore this symilarity maps ![]() to
to ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Hidden spiral symilarity
Let ![]() be an isosceles right triangle
be an isosceles right triangle ![]() Let
Let ![]() be a point on a circle with diameter
be a point on a circle with diameter ![]() The line
The line ![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]() and intersects
and intersects ![]() at
at ![]() Prove that
Prove that ![]()
Proof
Denote ![]()
![]() Let
Let ![]() cross perpendicular to
cross perpendicular to ![]() in point
in point ![]() at point
at point ![]()
Then ![]()
Points ![]() and
and ![]() are simmetric with respect
are simmetric with respect ![]() so
so ![]()
The spiral symilarity centered at ![]() with coefficient
with coefficient ![]() and the angle of rotation
and the angle of rotation ![]() maps
maps ![]() to
to ![]() and
and ![]() to point
to point ![]() such that
such that ![]()
Therefore ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
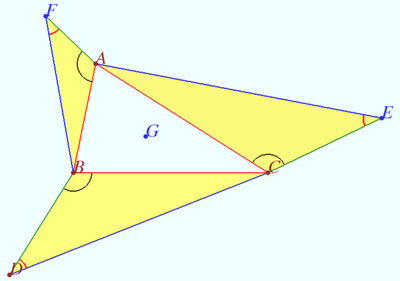
Linearity of the spiral symilarity
![]() Points
Points ![]() are outside
are outside ![]()
Prove that the centroids of triangles ![]() and
and ![]() are coinsite.
are coinsite.
Proof
Let ![]() where
where ![]() be the spiral similarity with
be the spiral similarity with ![]() and
and ![]() A vector has two parameters, modulo and direction. It is not tied to a center of the spiral similarity. Therefore
A vector has two parameters, modulo and direction. It is not tied to a center of the spiral similarity. Therefore ![]()
![]() We use the property of linearity and get
We use the property of linearity and get ![]() Let
Let ![]() be the centroid of
be the centroid of ![]() so
so ![]() is the centroid of the
is the centroid of the ![]()
vladimir.shelomovskii@gmail.com, vvsss