Afly's notes

About Afly

Friends with Yrock and ConfidentFlamingo

User # 1013218 Profile

Competitions I have participated in:

AMC8 * 1

AMC10A * 1

AMC10B * 1

MathLeague Qualifications * 7

MathLeague District * 2

MathLeague District Countdown * 1

MathLeague State * 1

MathLeague State Countdown * 1

MathLeague National * 1

MathLeague National Countdown * 1

MathLeague International * 1

Some of my asymptote creations

These are a random collection of diagrams and text that I have made. YOU ARE ALLOWED TO USE THESE IMAGES AND/OR TEXT IN YOUR PAGES OR USE THEM FOR REFERENCE.

I try to put them in the order of how much technique & technical points there are in them

Enough talking. Let's get into the pictures.

Triangle

Starring: Basic path drawing and LaTeX

$[asy] pair A=(0,0); pair B=(2,0); pair C=(1,sqrt(3)); draw(A--B--C); draw(A--C--B); [/asy]$

$\text{That is a equilateral triangle with side length 2!}$

$\text{The height is } \sqrt{2^2-1^2} = \sqrt{3}$

$\text{The area is } 2 \cdot \sqrt{3} \cdot \frac{1}{2} = \boxed{\sqrt{3}}$

$\dots$

$[asy] pair A=(0,0); pair B=(0,2); pair C=(1,1); draw(A--B--C); draw(A--C--B); [/asy]$

$\text{Homework: calculate the area}$

ANSWER: LOOK ONLY WHEN THE PROBLEM IS COMPLETED >>> THIS IS ONLY TO CHECK YOUR ANSWER

$\text{This is an isosceles right triangle. It has side length }\sqrt{2}$

$\text{It has an height of } \frac{\sqrt{2}}{\sqrt{2}} = 1 \text{ and a base of } \sqrt{2} \cdot \sqrt{2} = 2$

$\text{The area is } 1 \cdot 2 \cdot \frac{1}{2} = \boxed{1}$ +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Pythagorean

Starring: Colored paths and line width

$[asy] pair A=(0,0); pair B=(0,3); pair C=(4,0); draw(A--B--C--A,black+linewidth(1)); pair D=(-3,0); pair E=(-3,3); draw(A--B--E--D--A,red+linewidth(1)); pair F=(0,-4); pair G=(4,-4); draw(A--C--G--F--A,orange+linewidth(1)); pair H=(7,4); pair I=(3,7); draw(B--C--H--I--B,yellow+linewidth(1)); draw(A--B--C--A,black+linewidth(1)); [/asy]$ $\text{The pythagorean theorem: red plus orange equals yellow}$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Trapezoid

Starring: Filling regions

$[asy] pair A=(0,0); pair B=(10,0); pair C=(6,8); pair D=(2,8); pair E=(30/7,40/7); draw(A--B--C--D--A,black+linewidth(5)); fill(A--E--D--cycle,red); fill(B--E--C--cycle,yellow); dot(A); dot(B); dot(C); dot(D); dot(E); label(A,'A',SW); label(B,'B',SE); label(C,'C',NE); label(D,'D',NW); label(E,'E',S); draw(A--E--C,blue+linewidth(2)); draw(B--E--D,blue+linewidth(2)); [/asy]$ $\text{Given that } \overline{AB} \parallel \overline{DC} \text{ , prove that } A_\triangle AED = A_\triangle BEC .$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Hexagon (In AMC 2023 10A #24)

Starring: polygon(), shift(), dir(), unitsize, labels

$[asy] unitsize(5cm); draw(scale(3)*polygon(6)); filldraw(shift(dir(0)*2+dir(120)*3/7)*polygon(6), lightgray); filldraw(shift(dir(60)*2+dir(180)*3/7)*polygon(6), lightgray); filldraw(shift(dir(120)*2+dir(240)*3/7)*polygon(6), lightgray); filldraw(shift(dir(180)*2+dir(300)*3/7)*polygon(6), lightgray); filldraw(shift(dir(240)*2+dir(0)*3/7)*polygon(6), lightgray); filldraw(shift(dir(300)*2+dir(60)*3/7)*polygon(6), yellow); pair A = (0,0) + 3 * dir(300); pair B = A + 3/7 *dir(60); pair C = B + 1 * dir(180); pair D = C + 3/7 * dir(240); pair E = C + 4/7 * dir(120); pair F = E + 3/7 * dir(240); pair G = F + 4/7 * dir(240); pen p = red+linewidth(6); draw(A--B--C--D--cycle,p); draw(C--E--F--D--cycle,p); draw(F--G--D--cycle,p); label("1",(B + C)/2,dir(90)); label("1",(A + D)/2,dir(270)); label("3/7",(A + B)/2,dir(330)); label("3/7",(C + D)/2,dir(330)); label("4/7",(C+E)/2,dir(30)); label("3/7",(E+F)/2,dir(150)); label("4/7",(F+D)/2,dir(30)); label("4/7",(F+G)/2,dir(150)); label("4/7",(G+D)/2,dir(270)); [/asy]$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Tiny 2D experiments

Grid with numbers

Starring: Custom colors

$[asy] unitsize(36); pair A1 = (0,0); pair A2 = (0,5); pair A3 = (5,5); pair A4 = (5,0); fill(A1--A2--A3--A4--cycle,gray(0.61437908496)); draw(A1--A4--A4+dir(90)--A1+dir(90)--A1+dir(90)*2--A4+dir(90)*2--A3-dir(90)*2--A2-dir(90)*2--A2-dir(90)--A3-dir(90)--A3--A2,linewidth(3)); draw(A1--A2--A2+dir(0)--A1+dir(0)--A1+dir(0)*2--A2+dir(0)*2--A3-dir(0)*2--A4-dir(0)*2--A4-dir(0)--A3-dir(0)--A3--A4,linewidth(3)); pair B1 = (0,1/2); pair B2 = (0,3/2); pair B3 = (0,5/2); pair B4 = (0,7/2); pair B5 = (0,9/2); pair C1 = (1/2,0); pair C2 = (3/2,0); pair C3 = (5/2,0); pair C4 = (7/2,0); pair C5 = (9/2,0); label("0",B1+C1); label("0",B2+C1); label("0",B3+C1); label("0",B4+C1); label("0",B5+C1); label("0",B1+C2); label("0",B2+C2); label("0",B3+C2); label("1",B4+C2); label("1",B5+C2); label("0",B1+C3); label("0",B2+C3); label("2",B3+C3); label("1",B4+C3); label("0",B5+C3); label("0",B1+C4); label("5",B2+C4); label("3",B3+C4); label("0",B4+C4); label("0",B5+C4); label("7",B1+C5); label("1",B2+C5); label("0",B3+C5); label("2",B4+C5); label("0",B5+C5); [/asy]$

Tiny 3D experiments

Starring: Using cleverly placed colors and lines to make a illusion (just pure skill, not really Asymptote)

Cube

$[asy] unitsize(60); pair A = (0,0); pair B = A + dir(0); pair C = A + dir(60); pair D = A + dir(120); pair E = A + dir(180); pair F = A + dir(240); pair G = A + dir(300); filldraw(A--B--C--D--cycle,orange); filldraw(A--D--E--F--cycle,blue); filldraw(A--F--G--B--cycle,gray); [/asy]$

Smaller cube

$[asy] unitsize(40); pair A = (0,0); pair B = A + dir(0); pair C = A + dir(60); pair D = A + dir(120); pair E = A + dir(180); pair F = A + dir(240); pair G = A + dir(300); filldraw(A--B--C--D--cycle,orange); filldraw(A--D--E--F--cycle,blue); filldraw(A--F--G--B--cycle,gray); [/asy]$

Cube with a cube hole in it

$[asy] unitsize(60); pair A = (0,0); pair B = A + dir(0); pair b = A + 2/3*dir(0); pair C = A + dir(60); pair c = A + 2/3*dir(60); pair D = A + dir(120); pair d = A + 2/3*dir(120); pair E = A + dir(180); pair e = A + 2/3*dir(180); pair F = A + dir(240); pair f = A + 2/3*dir(240); pair G = A + dir(300); pair g = A + 2/3*dir(300); filldraw(A--e--f--g--cycle,orange); filldraw(A--g--b--c--cycle,blue); filldraw(A--c--d--e--cycle,gray); filldraw(b--c--d--D--C--B--cycle,orange); filldraw(d--e--f--F--E--D--cycle,blue); filldraw(f--g--b--B--G--F--cycle,gray); [/asy]$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Pascal's triangle mod

Starring: Loops and arrays

mod 2

int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
int[] d={};
pen p1=rgb(1/8,1/8,7/8);
pen p2=rgb(1/8,7/8,1/8);
for (int i=0; i<256; ++i)
{
 for (int j=0; j<i+1; ++j)
 {
  if (j==0 || i==j) {
   pascal[i].push(1);
  } else {
   pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
  }
  if (pascal[i][j]%2==0){
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
  } else {
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
  }
 }
}
 (Error making remote request. Unknown error_msg)

mod 3

$[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%3==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%3==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } } } } [/asy]$

mod 4

$[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); pen p4=rgb(7/8,7/8,1/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%4==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%4==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { if (pascal[i][j]%4==2) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4); } } } } } [/asy]$

mod 5

$[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); pen p4=rgb(7/8,7/8,1/8); pen p5=rgb(1/8,7/8,7/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%5==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%5==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { if (pascal[i][j]%5==2) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } else { if (pascal[i][j]%5==3) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p5); } } } } } } [/asy]$

Rotating cube

Starring: Asymptote three

Perspective

$[asy] import three; unitsize(3); currentprojection=perspective(2,0,1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(15),2*Sin(15),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(30),2*Sin(30),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(45),2*Sin(45),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(60),2*Sin(60),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(75),2*Sin(75),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

Orthographic

$[asy] import three; unitsize(3); currentprojection=orthographic(2,0,1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(15),2*Sin(15),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(30),2*Sin(30),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(45),2*Sin(45),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(60),2*Sin(60),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

$[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(75),2*Sin(75),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]$

Circle diagrams

A collection of stuff having to do with circles

Intersection points

Starring: Fancy labels, Troubleshooting

$[asy] unitsize(9); pair A1 = (0,0); pair A2 = A1 + dir(0)*30; pair A3 = A2 + dir(0)*30; pair B1 = (9,0); pair B2 = B1 + dir(0)*30; pair B3 = B2 + dir(0)*30; pair G1 = (9/2,-15/2); pair G2 = G1 + dir(0)*30; pair G3 = G2 + dir(0)*30; pair H1 = A1 + dir(90)*5; pair H2 = A2 + dir(90)*5; pair H3 = A3 + dir(90)*5; pair I1 = B1 + dir(90)*3; pair I2 = B2 + dir(90)*4; pair I3 = B3 + dir(90)*5; pair J1 = A1 + dir(120)*5; pair J2 = A2 + dir(120)*5; pair J3 = A3 + dir(120)*5; pair K1 = B1 + dir(60)*3; pair K2 = B2 + dir(60)*4; pair K3 = B3 + dir(60)*5; pair N1 = G1 + dir(270)*3; pair N2 = G2 + dir(270)*3; pair N3 = G3 + dir(270)*3; path E1 = circle(A1,5); path E2 = circle(A2,5); path E3 = circle(A3,5); path F1 = circle(B1,3); path F2 = circle(B2,4); path F3 = circle(B3,5); path L1 = A1--J1; path L2 = A2--J2; path L3 = A3--J3; path M1 = B1--K1; path M2 = B2--K2; path M3 = B3--K3; path O1 = A1--B1; path O2 = A2--B2; path O3 = A3--B3; draw(E1,red); draw(E2,red); draw(E3,red); draw(F1,green); draw(F2,green); draw(F3,green); draw(L1,red); draw(L2,red); draw(L3,red); draw(M1,green); draw(M2,green); draw(M3,green); draw(O1,blue); draw(O2,blue); draw(O3,blue); dot(A1); dot(A2); dot(A3); dot(B1); dot(B2); dot(B3); label("$O_{A1}$",A1,dir(240),red); label("$O_{A2}$",A2,dir(240),red); label("$O_{A3}$",A3,dir(240),red); label("$O_{B1}$",B1,dir(300),green); label("$O_{B2}$",B2,dir(300),green); label("$O_{B3}$",B3,dir(300),green); label("No points",G1); label("One point",G2); label("Two points",G3); label("$r_{A1}+r_{B1}<d_1$",N1); label("$r_{A2}+r_{B2}=d_2$",N2); label("$r_{A3}+r_{B3}>d_3$",N3); label("$r_{A1}$",L1,dir(210),red); label("$r_{A2}$",L2,dir(210),red); label("$r_{A3}$",L3,dir(210),red); label("$r_{B1}$",M1,dir(330),green); label("$r_{B2}$",M2,dir(330),green); label("$r_{B3}$",M3,dir(330),green); label("$d_1$",O1,dir(240),blue); label("$d_2$",O2,dir(240),blue); label("$d_3$",O3,dir(240),blue); pair [] D1 = intersectionpoints(E2,F2); pair [] D2 = intersectionpoints(E3,F3); pair C1 = D1[0]; pair C2 = D2[0]; pair C3 = D2[1]; dot(C1,blue); dot(C2,blue); dot(C3,blue); label("$I_2$",C1,dir(315),blue); label("$I_{3a}$",C2,dir(0),blue); label("$I_{3b}$",C3,dir(0),blue); [/asy]$

Created files

(Using desmos)

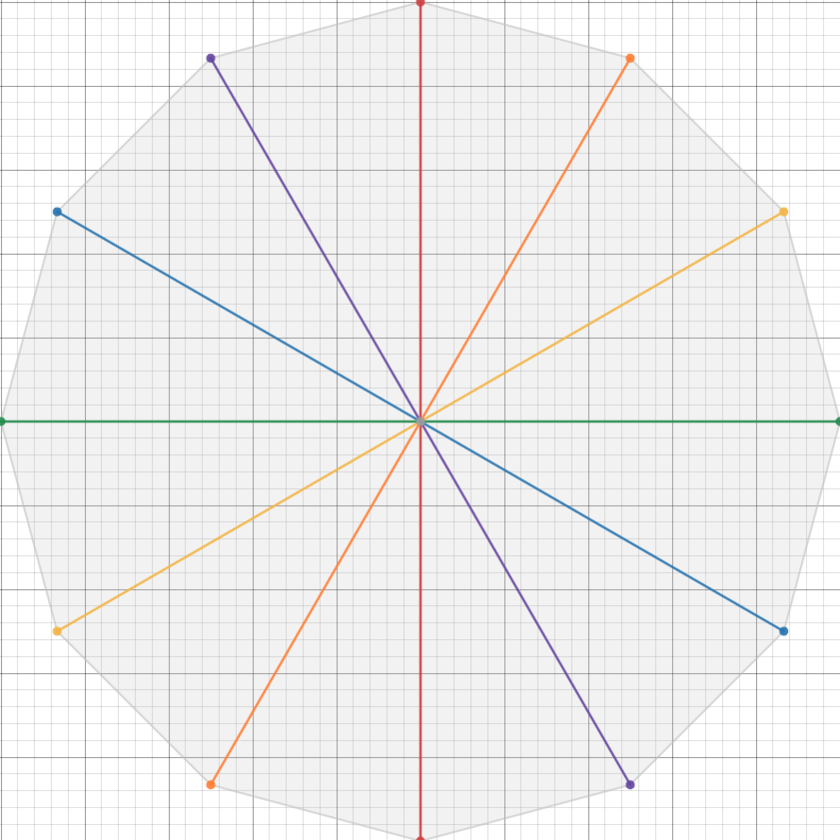
Colored dodecagon

Original file:

File

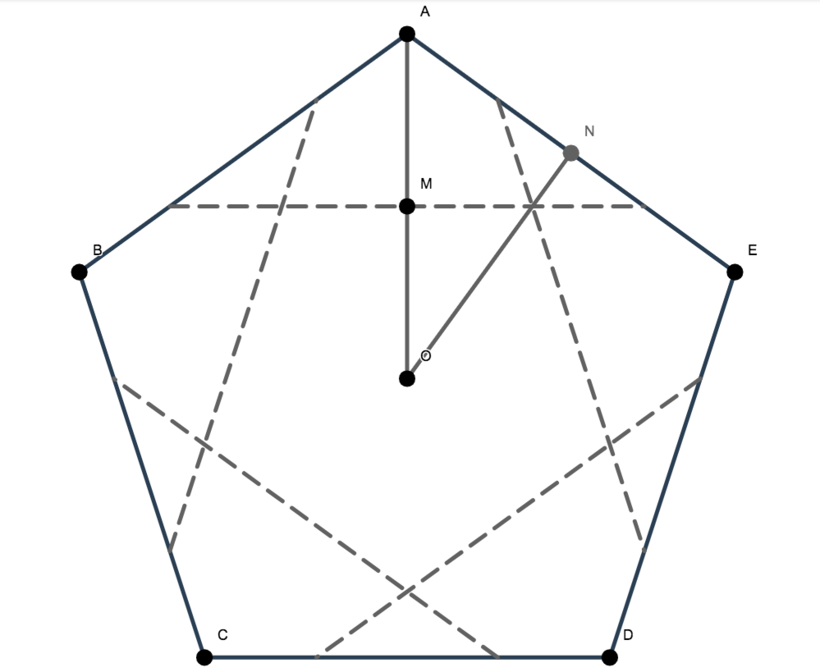
Pentagon 2023 12B Q25 dissmo

Original size:

File

LaTeX Creations (coming soon!)

Solutions created

2019 AIME II #5 Solution 7(Generating functions)

Let's look at the prime factorization of some of these rolls:

 01 => 2^0*3^0*5^0
 02 => 2^1*3^0*5^0
 03 => 2^0*3^1*5^0
 04 => 2^2*3^0*5^0
 05 => 2^0*3^0*5^1
 06 => 2^1*3^1*5^0

Now, using multi-variable generating functions, we get:

 f(x,y,z)=1+x+y+x^2+z+xy
            | |
           \| |/
            'v'
 f(x,y,z)=1+x+y+z+x^2+xy
   =(for our purposes)
       =2+x+y+z+xy

Let's square that!

 4+2x+2y+2z+2xy+2x+x^2+xy+xz+x^2y+2y+xy+y^2+yz+xy^2+2z+xz+yz+z^2+xyz+2xy+x^2y+xy^2+xyz+x^2y^2
 Combining like terms . . .
 4+4x+4y+4z+x^2+y^2+z^2+6xy+2xz+2yz+2xyz+2x^2y+2xy^2+x^2y^2

Since we only want the parity of each of the exponents, we can collapse it again.

 8+6x+6y+4z+6xy+2xz+2yz+2xyz

Last simplification: factor out a factor of two and save it for later.

 4+3x+3y+2z+3xy+xz+yz+xyz

Let's take a better approach this time.

 ___ term :4*4+3*3+3*3+2*2+3*3+1*1+1*1+1*1=16+09+09+04+09+01+01+01=50
 __x term :4*3+3*4+3*3+2*1+3*3+1*2+1*1+1*1=12+12+09+02+09+02+01+01=48
 __y term :4*3+3*3+3*4+2*1+3*3+1*1+1*2+1*1=12+09+12+02+09+01+02+01=48
 __z term :4*2+3*1+3*1+2*4+3*1+1*3+1*3+1*3=08+03+03+08+03+03+03+03=34
 _xy term :4*3+3*3+3*3+2*1+3*4+1*1+1*1+1*2=12+09+09+02+12+01+01+02=48
 _xz term :4*1+3*2+3*1+2*3+3*1+1*4+1*3+1*3=04+06+03+06+03+04+03+03=32
 _yz term :4*1+3*1+3*2+2*3+3*1+1*3+1*4+1*3=04+03+06+06+03+03+04+03=32
 xyz term :4*1+3*1+3*1+2*3+3*2+1*3+1*3+1+4=04+03+03+06+06+03+03+04=32
 
 Result: 50+48x+48y+34z+48xy+32xz+32yz+32xyz

I know we could use vectors and dot products to make it look neater but come on. It already looks neat enough. Also, we didn't need the other parts, but it just looks nicer. Now let's stick back the two that turned into a four.

 200+192x+192y+136z+192xy+128xz+128yz+128xyz

We seek the constant term which is 200. 200/1296=100/648=50/324=25/162, 25+162=187

Yrock's Notes

ConfidentFlamingo's notes

Other Users' notes

Note from afly: If you leave a note, write who it is from

Page

Toolbox

Search

User:Afly

Contents

Afly's notes

About Afly

Some of my asymptote creations

Triangle

Pythagorean

Trapezoid

Hexagon (In AMC 2023 10A #24)

Tiny 2D experiments

Grid with numbers

Tiny 3D experiments

Cube

Smaller cube

Cube with a cube hole in it

Pascal's triangle mod

mod 2

mod 3

mod 4

mod 5

Rotating cube

Perspective

Orthographic

Circle diagrams

Intersection points

Created files

Colored dodecagon

Pentagon 2023 12B Q25 dissmo

LaTeX Creations (coming soon!)

Solutions created

2019 AIME II #5 Solution 7(Generating functions)

Yrock's Notes

ConfidentFlamingo's notes

Other Users' notes