2024 AMC 8 Problems/Problem 15
Problem
Solution
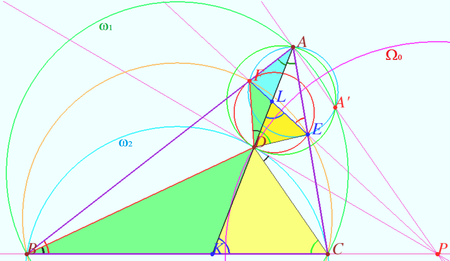
We prove that circles ![]() and
and ![]() centered at
centered at ![]() (the intersection point
(the intersection point ![]() and
and ![]() have a common chord. Let
have a common chord. Let ![]() be the intersection point of the tangent to the circle
be the intersection point of the tangent to the circle ![]() at the point
at the point ![]() and the line
and the line ![]() is inverse to
is inverse to ![]() with respect to the circle
with respect to the circle ![]() centered at
centered at ![]() with radius
with radius ![]() Then the pairs of points
Then the pairs of points ![]() and
and ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() , so the points
, so the points ![]() and
and ![]() are collinear. Quadrilaterals containing the pairs of inverse points
are collinear. Quadrilaterals containing the pairs of inverse points ![]() and
and ![]() and
and ![]() and
and ![]() are inscribed,
are inscribed, ![]() is antiparallel to
is antiparallel to ![]() with respect to angle
with respect to angle ![]() (see
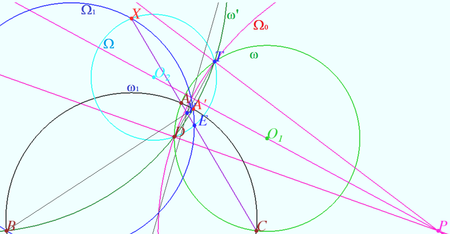
(see ![]() ). Consider the circles
). Consider the circles ![]() centered at
centered at ![]()
![]() centered at
centered at ![]() and
and ![]() Denote
Denote ![]() . Then
. Then ![]()
![]() is cyclic),
is cyclic), ![]() is cyclic,
is cyclic, ![]() is antiparallel),
is antiparallel), ![]()
![]() is the point of the circle
is the point of the circle ![]() Let the point
Let the point ![]() be the radical center of the circles
be the radical center of the circles ![]() It has the same power
It has the same power ![]() with respect to these circles. The common chords of the pairs of circles
with respect to these circles. The common chords of the pairs of circles ![]() where
where ![]() intersect at this point.
intersect at this point. ![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() is the radical axis of
is the radical axis of ![]()
![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() containing
containing ![]() is the radical axis of
is the radical axis of ![]() and
and ![]() Hence
Hence ![]() has power
has power ![]() with respect to
with respect to ![]() Let
Let ![]() be the point of intersection
be the point of intersection ![]() Since the circles
Since the circles ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() then
then ![]() lies on
lies on ![]() and
and ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]() The power of a point
The power of a point ![]() with respect to the circles
with respect to the circles ![]() and
and ![]() are the same,
are the same, ![]() the points
the points ![]() and
and ![]() coincide. The centers of the circles
coincide. The centers of the circles ![]() and
and ![]() (
(![]() and
and ![]() ) are located on the perpendicular bisector
) are located on the perpendicular bisector ![]() , the point
, the point ![]() is located on the perpendicular bisector
is located on the perpendicular bisector ![]() and, therefore, the points
and, therefore, the points ![]() and
and ![]() lie on a line, that is, the lines
lie on a line, that is, the lines ![]() and
and ![]() are concurrent.
are concurrent.
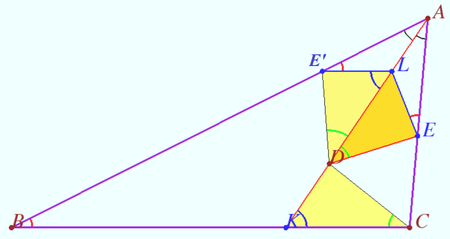
![]() Let
Let ![]() be bisector of the triangle
be bisector of the triangle ![]() , point
, point ![]() lies on
lies on ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() . The point
. The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() Let
Let ![]() be the intersection point of the tangent to the circle
be the intersection point of the tangent to the circle ![]() at the point
at the point ![]() and the line
and the line ![]() Let the circle
Let the circle ![]() be centered at
be centered at ![]() and has the radius
and has the radius ![]() Then the pairs of points
Then the pairs of points ![]() and
and ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() and
and ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]()
![]() Let the point
Let the point ![]() is symmetric to
is symmetric to ![]() with respect to bisector
with respect to bisector ![]() Symmetry of points
Symmetry of points ![]() and
and ![]() implies
implies ![]()
![]()
![]()
![]()
![]() Similarly, we prove that
Similarly, we prove that ![]() and
and ![]() are antiparallel with respect to angle
are antiparallel with respect to angle ![]() and the points
and the points ![]() in triangles
in triangles ![]() and
and ![]() coincide. Hence,
coincide. Hence, ![]() and
and ![]() are antiparallel and
are antiparallel and ![]() is cyclic. Note that
is cyclic. Note that ![]() and
and ![]()
![]() so
so ![]() is tangent to the circle
is tangent to the circle ![]()
![]() that is, the points
that is, the points ![]() and
and ![]() and
and ![]() are inverse with respect to the circle
are inverse with respect to the circle ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
(This was on the page of the 2021 IMO problem 3) Yes this person actually solved it. I just copy pasted for people that want to know. -Multpi12)