Surface of constant width

A curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. A surface of constant width (orbiform) is a convex form whose width, measured by the distance between two opposite parallel planes touching its boundary, is the same regardless of the direction of those two parallel planes.

Reuleaux triangle

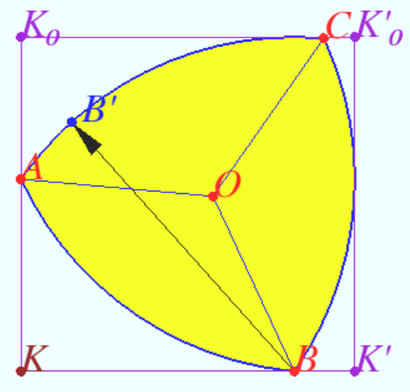
The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle.

Let be equilateral triangle.

Let be the arc centered at with radius

Arcs and define similarly.

All points on this arcs are equidistant from the opposite vertex. Distance is