Disphenoid
Disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles.
Main
a) A tetrahedron ![]() is a disphenoid iff
is a disphenoid iff ![]()
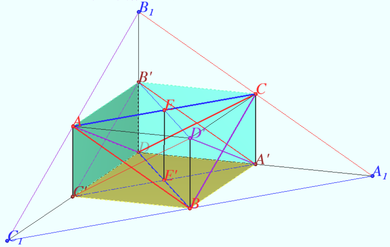
b) A tetrahedron is a disphenoid iff its circumscribed parallelepiped is right-angled.
c) Let ![]() The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are:
The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are:
![]()
![]() The circumscribed sphere has radius (the circumradius):
The circumscribed sphere has radius (the circumradius):
![]()
The volume of a disphenoid is:
![]() Each height of disphenoid
Each height of disphenoid ![]() is
is ![]() the inscribed sphere has radius:
the inscribed sphere has radius: ![]() where
where ![]() is the area of
is the area of ![]()
Proof
a) ![]()
![]() because in
because in ![]() there is no equal sides.
there is no equal sides.
Let consider ![]()
![]() but one of sides need be equal
but one of sides need be equal ![]() so
so ![]()
b) Any tetrahedron can be assigned a parallelepiped by drawing a plane through each edge of the tetrahedron parallel to the opposite edge.
![]() is parallelogram with equal diagonals, i.e. rectangle.
is parallelogram with equal diagonals, i.e. rectangle.
Similarly, ![]() and
and ![]() are rectangles.
are rectangles.
If ![]() is rectangle, then
is rectangle, then ![]()
Similarly, ![]() is a disphenoid.
is a disphenoid.
c) ![]()
Similarly, ![]()
![]()
Similarly, ![]()
Let ![]() be the midpoint
be the midpoint ![]() ,
, ![]() be the midpoint
be the midpoint ![]()
![]() is the bimedian of
is the bimedian of ![]() and
and ![]()
![]()
The circumscribed sphere of ![]() is the circumscribed sphere of
is the circumscribed sphere of ![]() so it is
so it is
![]()
The volume of a disphenoid is third part of the volume of ![]() so:
so:
![]() The volume of a disphenoid is
The volume of a disphenoid is ![]() where
where ![]() is any height.
is any height.
The inscribed sphere has radius ![]()
![]()
![]()
![]()
![]()
Therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss