Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2006 AMC 10B Problems/Problem 24

Revision as of 18:20, 12 August 2006 by Xantos C. Guin (talk | contribs) (fixed link)

Problem

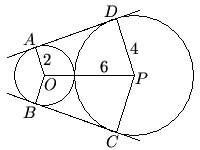
Circles with centers $O$ and $P$ have radii $2$ and $4$, respectively, and are externally tangent. Points $A$ and $B$ on the circle with center $O$ and points $C$ and $D$ on the circle with center $P$ are such that $AD$ and $BC$ are common external tangents to the circles. What is the area of the concave hexagon $AOBCPD$?

2006amc10b24.gif

$\mathrm{(A) \ } 18\sqrt{3}\qquad \mathrm{(B) \ } 24\sqrt{2}\qquad \mathrm{(C) \ } 36\qquad \mathrm{(D) \ } 24\sqrt{3}\qquad \mathrm{(E) \ } 32\sqrt{2}$

Solution

Since a tangent line is perpendicular to the radius containing the tangent point, $\angle OAD = \angle PDA = 90^\circ$.

Construct a perpendicular to $DP$ that goes through point $O$. Label the point of intersection $X$.

Clearly $OADX$ is a rectangle.

Therefore $DX=2$ and $PX=2$.

By the Pythagorean Theorem: $OX = \sqrt{6^2 - 2^2} = 4\sqrt{2}$.

The area of $OADX$ is $2\cdot4\sqrt{2}=8\sqrt{2}$.

The area of $OXP$ is $\frac{1}{2}\cdot2\cdot4\sqrt{2}=4\sqrt{2}$.

So the area of quadrilateral $OADP$ is $8\sqrt{2}+4\sqrt{2}=12\sqrt{2}$.

Using similar steps, the area of quadrilateral $OBCP$ is also $12\sqrt{2}$

Therefore, the area of hexagon $AOBCPD$ is $2\cdot12\sqrt{2}= 24\sqrt{2} \Rightarrow B$

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_24&oldid=9465"