2018 IMO Problems/Problem 1

Let be the circumcircle of acute triangle . Points and are on segments and respectively such that . The perpendicular bisectors of and intersect minor arcs and of at points and respectively. Prove that lines and are either parallel or they are the same line.

-- solution --

http://wiki-images.artofproblemsolving.com/5/5d/FB_IMG_1531446409131.jpg

The diagram is certainly not to scale, but the argument is sound (I believe) and involves re-ordering the construction as specified in the original problem so that an identical state of affairs results, yet in so doing differently it is made clear that the line segments in question are parallel.

Construct a right-angled triangle ABC'. Select an arbitrary point H along the segment BC', and from point H select an arbitrary point F such that the segment HF is perpendicular to the segment AB. Mark the distance from the intersection of HF and AB to B at B" (i.e., HF is a perpendicular bisector). It follows that the triangle B"FB is isosceles. Construct an isosceles triangle FHG. Mark the distance of AB" along AC' at C". (From here, a circle can be constructed according to the sets of points A, B, F, and A, B, G. Points F and G may be repositioned to allow for these circles to coincide; also, point H may be repositioned so that point C falls on the coinciding circle, understood that HG is the other perpendicular bisector.)

Assign the angle BAC the value α. Hence, the angle FHG has the value 180°-α, and the angle HFG (also, HGF) has the value α/2. Assign the angle BFH the value β. Hence, the angle B'FB" has the value β-α/2. Consequently, the angle FB'B" has the value 180°-(β-α/2)-(90°-β) = 90°+α/2, and so too its vertical angle BB'G. As the triangle B"AC" is isosceles, and its subtended angle has the value α, the angles BB"C" and CC"B" both have the value 90°+α/2. It follows therefore that segments B"C" and FG are parallel.

(N.B. Points D and E, as given in the wording of the original problem, have been renamed B" and C" here.)

Solution 2

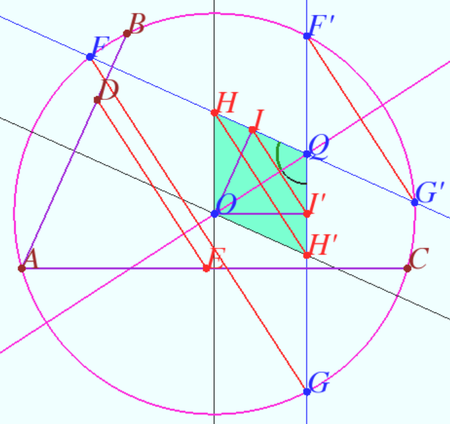
The essence of the proof is using a rhombus formed by the perpendicular bisectors of the segments and and the parallelism of its diagonal and the base of the triangle formed by the perpendiculars from one vertex of the rhombus.

The perpendicular bisectors of the segments and intersect at points (the circumcenter and Let The distance from the line to point is from to is Therefore, the distance between lines and is Similarly, the distance between the lines and is

The quadrilateral is formed by the intersection of two pairs of equidistant lines is a parallelogram with equal heights is a rhombus.

Let and be the bases of the heights of the rhombus from the vertex In isosceles triangles and the sides are parallel, hence the bases of these triangles are parallel, The bases of the heights and divide the sides of the rhombus in the same ratio, which means that the diagonal of the rhombus is parallel to the segments

The angles between the diagonal of the rhombus and its sides are the same, so The lines and are symmetrical with respect to the diameter so The homothety of triangles and centered at implies Therefore, these three lines are parallel to

Note that triangle may be obtuse.

vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru